题目内容
15. 如图,在四边形ABCD中,AB=AD=2$\sqrt{3}$,BC=CD=2,∠BAD=60°,点M为线段AD的中点,将△DMC沿线段MC翻折到△PMC(点D与点P重合),使得平面PAC⊥平面ABCD,连接PA、PB.
如图,在四边形ABCD中,AB=AD=2$\sqrt{3}$,BC=CD=2,∠BAD=60°,点M为线段AD的中点,将△DMC沿线段MC翻折到△PMC(点D与点P重合),使得平面PAC⊥平面ABCD,连接PA、PB.(1)在AB上是否存在一点N,使得PC⊥平面PMN?若存在,指出点N的位置并加以证明,若不存在,请说明理由;
(2)求二面角P-MC-B的正切值.
分析 (1)根据线面垂直的判定定理,结合图象折叠前后的位置关系进行判断即可.
(2)建立坐标系,利用向量法即可求二面角P-MC-B的正切值.
解答  解:(1)∵在四边形ABCD中,AB=AD=2$\sqrt{3}$,BC=CD=2,∠BAD=60°,
解:(1)∵在四边形ABCD中,AB=AD=2$\sqrt{3}$,BC=CD=2,∠BAD=60°,
∴连接AC,BD相交于O,
则O为BD的中点,且AO⊥BD,
∵∠BAD=60°,∴∠CAD=30°,
则AD⊥CD,即MP⊥PC,
∵将△DMC沿线段MC翻折到△PMC(点D与点P重合),使得平面PAC⊥平面ABCD,
∴PO⊥平面ABC,
AO=3,CO=1,DO=OB=OP=$\sqrt{3}$,
在AB上若存在一点N,使得PC⊥平面PMN,
则∵PC⊥MP,
∴只需要PC⊥MN,即可,
即MN⊥平面PAC即可,MN⊥AO,
∵M为线段AD的中点,
∴N为线段AB的中点,
即当N为线段AB的中点时,满足PC⊥平面PMN.
(2)以O为坐标原点,OA,OB,OP分别为x,y,z轴,建立空间坐标系如图:
则A(3,0,0),B(0,$\sqrt{3}$,0),P(0,0,$\sqrt{3}$),D(0,-$\sqrt{3}$,0),
M($\frac{3}{2}$,$-\frac{\sqrt{3}}{2}$,0),C(-1,0,0)
设平面PMC的法向量为$\overrightarrow{m}$=(x,y,z),
则$\overrightarrow{PM}$=($\frac{3}{2}$,$-\frac{\sqrt{3}}{2}$,-$\sqrt{3}$),$\overrightarrow{PC}$=(-1,0,-$\sqrt{3}$),
由$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{PM}=0}\\{\overrightarrow{m}•\overrightarrow{PC}=0}\end{array}\right.$得$\left\{\begin{array}{l}{\frac{3}{2}x-\frac{\sqrt{3}}{2}y-\sqrt{3}z=0}\\{-x-\sqrt{3}z=0}\end{array}\right.$,
令x=$\sqrt{3}$,则y=1,z=-1,
即$\overrightarrow{m}$=($\sqrt{3}$,1,-1),
平面MBC的法向量为$\overrightarrow{n}$=(0,0,1),
则cos<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{-1}{1×\sqrt{3+1+1}}=-\frac{1}{\sqrt{5}}$,
∵二面角P-MC-B为锐二面角,
∴设二面角为θ,
则cosθ=$\frac{1}{\sqrt{5}}$,sinθ=$\frac{2}{\sqrt{5}}$,
则tanθ=2,
即二面角P-MC-B的正切值为2.
点评 本题主要考查空间线面垂直的判定以及二面角的求解,建立空间坐标系,利用向量法是解决本题的关键.

| A. | 2 | B. | 3 | C. | 6 | D. | 4 |
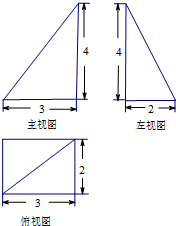
| A. | 24 | B. | 16 | C. | 12 | D. | 8 |
附表:
| P(k2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 95% | B. | 5% | C. | 97.5% | D. | 2.5% |
 如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,PE=2BE.
如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,PE=2BE.