题目内容
10．已知$\frac{{C}_{n-1}^{5}+{C}_{n-3}^{3}}{{C}_{n-3}^{3}}$=3$\frac{4}{5}$，求n的值．分析 根据题意，将$\frac{{C}_{n-1}^{5}+{C}_{n-3}^{3}}{{C}_{n-3}^{3}}$=3$\frac{4}{5}$变形可得5${C}_{n-1}^{5}$=14${C}_{n-3}^{3}$，利用组合数公式展开可得n2-3n-54=0，解可得答案．
解答 解：已知$\frac{{C}_{n-1}^{5}+{C}_{n-3}^{3}}{{C}_{n-3}^{3}}$=3$\frac{4}{5}$，则5${C}_{n-1}^{5}$=14${C}_{n-3}^{3}$，
展开可得：$\frac{（n-1）（n-2）（n-3）（n-4）（n-5）}{5×4×3×2×1}$=$\frac{（n-3）（n-4）（n-5）}{3×2×1}$，
变形可得（n-1）（n-2）=56，
即n2-3n-54=0，
解可得，n=9或n=-6（舍）；
答：n值为9．
点评 本题考查组合数公式的应用，注意牢记组合数公式，并熟练应用即可．
练习册系列答案
相关题目
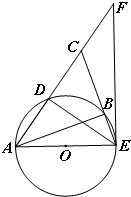如图，AE是⊙O直径，D是⊙O上一点，连结AD并延长使AD=DC，连结CE交⊙O于点B，连结AB．过点E的直线与AC的延长线交于点F，且∠F=∠CED．
如图，四棱锥S-ABCD中，AB∥CD，BC⊥CD，CD=$\frac{1}{2}$AB=$\frac{1}{2}$BC，若CD=1，SD=$\sqrt{7}$，且SA=SB=2．
如图，在四边形ABCD中，AB=AD=2$\sqrt{3}$，BC=CD=2，∠BAD=60°，点M为线段AD的中点，将△DMC沿线段MC翻折到△PMC（点D与点P重合），使得平面PAC⊥平面ABCD，连接PA、PB．
如图，三个半径都是5cm的小球放在一个半球面的碗中，三个小球的顶端恰好与碗的上沿处于同一水平面，则这个碗的半径R是5$+\frac{5\sqrt{21}}{3}$cm．