题目内容
18.已知直线l1∥l2,A是l1,l2之间的一定点,并且A点到l1,l2的距离分别为2,3,B是直线l2上一动点,作AC⊥AB,且使AC与直线l1交于点C,则△ABC面积的最小值为( )| A. | 2 | B. | 3 | C. | 6 | D. | 4 |
分析 用θ表示∠ABM,如图,通过解RT△ABM,RT△ABM 表示出AB,AC,利用S=$\frac{1}{2}$AB•AC将S表示为关于θ的三角函数,利用三角函数性质求出最值
解答 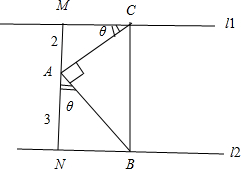 解:过A作l1,l2之间的垂线,垂足分别为M,N.设∠ABM=θ(0<θ<$\frac{π}{2}$),
解:过A作l1,l2之间的垂线,垂足分别为M,N.设∠ABM=θ(0<θ<$\frac{π}{2}$),
在RT△ACM中,sinθ=$\frac{2}{AC}$,∴AC=$\frac{2}{sinθ}$,同理可得AB=$\frac{3}{cosθ}$,
∴△ABC的面积S=$\frac{1}{2}$•AB•AC=$\frac{6}{sin2θ}$,
故当 2θ=90°,即θ=45°时,S取得最小值6,
故选:C.
点评 本题考查解三角形知识,函数思想、建模解模.考查分析、解决、计算能力,属于基础题.

练习册系列答案
相关题目
8.不等式组$\left\{\begin{array}{l}-2≤x≤2\\ 0≤y≤4\end{array}\right.$表示的点集记为M,不等式组$\left\{\begin{array}{l}x-y+2≥0\\ y={x^2}\end{array}\right.$表示的点集记为N,在M中任取一点P,则P∈N的概率为( )
| A. | $\frac{7}{16}$ | B. | $\frac{9}{16}$ | C. | $\frac{7}{32}$ | D. | $\frac{9}{32}$ |
9.从0,1,3,4,5,6六个数字中,选出一个偶数和两个奇数,组成一个没有重复数字的三位奇数,这样的三位数共有( )
| A. | 24个 | B. | 30个 | C. | 36个 | D. | 48个 |
6.已知等比数列{an}的各项都是正数,且3a1,$\frac{1}{2}$a3,2a2成等差数列,则$\frac{{a}_{20}+{a}_{19}}{{a}_{18}+{a}_{17}}$=( )
| A. | 1 | B. | 3 | C. | 6 | D. | 9 |
10.设实数a,b满足lg(a-1)+lg(b-2)=lg2,则a+b的取值范围是( )
| A. | (3,+∞) | B. | [3+2$\sqrt{2}$,+∞) | C. | (2,+∞) | D. | (2$\sqrt{2}$,+∞) |
7. 如图,每个底边为2的等腰三角形顶角的顶点都在反比例函数y=$\frac{6}{x}$(x>0)的图象上,第1个等腰三角形顶角的顶点横坐标为1,第2个等腰三角形的顶点横坐标为3,…以此类推,用含n的式子表示第n个等腰三角形底边上的高为( )
如图,每个底边为2的等腰三角形顶角的顶点都在反比例函数y=$\frac{6}{x}$(x>0)的图象上,第1个等腰三角形顶角的顶点横坐标为1,第2个等腰三角形的顶点横坐标为3,…以此类推,用含n的式子表示第n个等腰三角形底边上的高为( )
 如图,每个底边为2的等腰三角形顶角的顶点都在反比例函数y=$\frac{6}{x}$(x>0)的图象上,第1个等腰三角形顶角的顶点横坐标为1,第2个等腰三角形的顶点横坐标为3,…以此类推,用含n的式子表示第n个等腰三角形底边上的高为( )
如图,每个底边为2的等腰三角形顶角的顶点都在反比例函数y=$\frac{6}{x}$(x>0)的图象上,第1个等腰三角形顶角的顶点横坐标为1,第2个等腰三角形的顶点横坐标为3,…以此类推,用含n的式子表示第n个等腰三角形底边上的高为( )| A. | $\frac{6}{2n-1}$ | B. | $\frac{6}{{2}^{n+1}}$ | C. | $\frac{6}{2n+1}$ | D. | $\frac{6}{{2}^{n-1}}$ |
 如图,某商业中心O有通往正东方向和北偏东30°方向的两条街道,某公园P位于商业中心北偏东θ角(0<θ<$\frac{π}{2}$,tanθ=3$\sqrt{3}$),且与商业中心O的距离为$\sqrt{21}$公里处,现要经过公园P修一条直路分别与两条街道交汇于A,B两处,当商业中心O到A,B两处的距离之和最小时,A,B的距离为3$\sqrt{3}$公里.
如图,某商业中心O有通往正东方向和北偏东30°方向的两条街道,某公园P位于商业中心北偏东θ角(0<θ<$\frac{π}{2}$,tanθ=3$\sqrt{3}$),且与商业中心O的距离为$\sqrt{21}$公里处,现要经过公园P修一条直路分别与两条街道交汇于A,B两处,当商业中心O到A,B两处的距离之和最小时,A,B的距离为3$\sqrt{3}$公里. 如图,在四边形ABCD中,AB=AD=2$\sqrt{3}$,BC=CD=2,∠BAD=60°,点M为线段AD的中点,将△DMC沿线段MC翻折到△PMC(点D与点P重合),使得平面PAC⊥平面ABCD,连接PA、PB.
如图,在四边形ABCD中,AB=AD=2$\sqrt{3}$,BC=CD=2,∠BAD=60°,点M为线段AD的中点,将△DMC沿线段MC翻折到△PMC(点D与点P重合),使得平面PAC⊥平面ABCD,连接PA、PB.