Question

3．如图，在四棱锥P-ABCD中，PC⊥底面ABCD，底面ABCD是直角梯形，AB⊥AD，AB∥CD，AB=2AD=2CD=2，PE=2BE．
（I）求证：平面EAC⊥平面PBC；
（Ⅱ）若二面角P-AC-E的余弦值为$\frac{{\sqrt{6}}}{3}$，求直线PA与平面EAC所成角的正弦值．

Answer 1

分析 （I）由PC⊥底面ABCD，可得PC⊥AC．由AB=2，AD=CD=1，利用勾股定理的逆定理可得：AC⊥BC，因此AC⊥平面PBC，即可证明平面EAC⊥平面PBC．
（II）取AB的中点F，两角CF，则CF⊥AB，以点C为原点，建立空间直角坐标系，可得设P（0，0，a）（a＞0），可取$\overrightarrow{m}$=（1，-1，0），利用向量垂直与数量积的关系可得：$\overrightarrow{m}$为平面PAC的法向量．设$\overrightarrow{n}$=（x，y，z）为平面EAC的法向量，则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{EA}=0}\\{\overrightarrow{n}•\overrightarrow{CE}=0}\end{array}\right.$，可得$\overrightarrow{n}$，由于二面角P-AC-E的余弦值为$\frac{{\sqrt{6}}}{3}$，可得$|cos＜\overrightarrow{m}，\overrightarrow{n}＞|$=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{\sqrt{6}}{3}$，解得a=4．设直线PA与平面EAC所成角为θ，则sinθ=|$cos＜\overrightarrow{PA}，\overrightarrow{n}＞$|=$\frac{|\overrightarrow{PA}•\overrightarrow{n}|}{|\overrightarrow{PA}||\overrightarrow{n}|}$即可得出．

解答 （I）证明：∵PC⊥底面ABCD，AC?平面ABCD，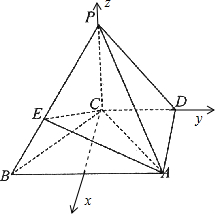
∴PC⊥AC．
∵AB=2，AD=CD=1，∴AC=BC=$\sqrt{2}$，∴AC²+BC²=AB²，
∴AC⊥BC，又BC∩PC=C，
∴AC⊥平面PBC，又AC?平面EAC，
∴平面EAC⊥平面PBC．
（II）解：取AB的中点F，两角CF，则CF⊥AB，以点C为原点，建立空间直角坐标系，
可得：C（0，0，0），A（1，1，0），B（1，-1，0），
设P（0，0，a）（a＞0），则E$（\frac{2}{3}，-\frac{2}{3}，\frac{a}{3}）$，
$\overrightarrow{CA}$=（1，1，0），$\overrightarrow{CP}$=（0，0，a），$\overrightarrow{CE}$=$（\frac{2}{3}，-\frac{2}{3}，\frac{a}{3}）$，
取$\overrightarrow{m}$=（1，-1，0），则$\overrightarrow{m}•\overrightarrow{CP}=\overrightarrow{m}•\overrightarrow{CA}$=0，
∴$\overrightarrow{m}$为平面PAC的法向量．
设$\overrightarrow{n}$=（x，y，z）为平面EAC的法向量，则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{EA}=0}\\{\overrightarrow{n}•\overrightarrow{CE}=0}\end{array}\right.$，即$\left\{\begin{array}{l}{x+y=0}\\{2x-2y+az=0}\end{array}\right.$，
取$\overrightarrow{n}$=（a，-a，-4），
∵二面角P-AC-E的余弦值为$\frac{{\sqrt{6}}}{3}$，
∴$|cos＜\overrightarrow{m}，\overrightarrow{n}＞|$=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{2a}{\sqrt{2}×\sqrt{2{a}^{2}+16}}$=$\frac{\sqrt{6}}{3}$，解得a=4，
∴$\overrightarrow{n}$=（4，-4，-4），$\overrightarrow{PA}$=（1，1，-4）．
设直线PA与平面EAC所成角为θ，则sinθ=|$cos＜\overrightarrow{PA}，\overrightarrow{n}＞$|=$\frac{|\overrightarrow{PA}•\overrightarrow{n}|}{|\overrightarrow{PA}||\overrightarrow{n}|}$=$\frac{16}{\sqrt{18}×\sqrt{16×3}}$=$\frac{2\sqrt{6}}{9}$，
∴直线PA与平面EAC所成角的正弦值为$\frac{2\sqrt{6}}{9}$．

点评 本题考查了线面面面垂直的判定与性质定理、等腰三角形的性质、勾股定理的逆定理、向量垂直与数量积的关系、利用法向量求空间角，考查了推理能力与计算能力，属于中档题．