Question

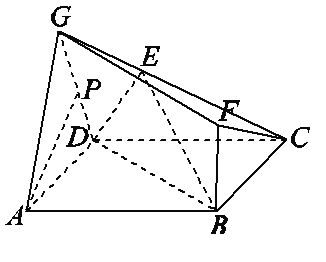
【题目】如图所示的多面体中，底面ABCD为正方形，△GAD为等边三角形，BF⊥平面ABCD，∠GDC＝90°，点E是线段GC上除两端点外的一点，若点P为线段GD的中点．

(Ⅰ)求证：AP⊥平面GCD；

(Ⅱ)求证：平面ADG∥平面FBC；

(Ⅲ)若AP∥平面BDE，求的值．

Answer 1

【答案】(1)见解析(2)见解析（3）2

【解析】试题分析：(1) 因为△GAD是等边三角形，点P为线段GD的中点，故AP⊥GD，又CD⊥平面GAD，所以CD⊥AP，从而AP⊥平面GCD.；(2) ∵BF⊥平面ABCD，∴BF⊥CD，又CD∩GD＝D， ∴CD⊥平面FBC，结合（1）可证明结果；(3) 连接PC交DE于点M，连接AC交BD于点O，连接OM，∵AP∥平面BDE，AP∥OM，从而M是PC中点，过P作PN∥DE，交CG于点N，

则N是GE中点，E是CN中点.

试题解析：

(Ⅰ)证明：因为△GAD是等边三角形，点P为线段GD的中点，故AP⊥GD，

因为AD⊥CD，GD⊥CD，且AD∩GD＝D，AD，GD平面GAD，故CD⊥平面GAD，

又AP平面GAD，故CD⊥AP，

又CD∩GD＝D，CD，GD平面GCD，故AP⊥平面GCD.

(Ⅱ)证明：∵BF⊥平面ABCD，∴BF⊥CD，

∵BC⊥CD，BF∩BC＝B，BF，BC平面FBC，∴CD⊥平面FBC，

由(Ⅰ)知CD⊥平面GAD，∴平面ADG∥平面FBC.

(Ⅲ)解：连接PC交DE于点M，连接AC交BD于点O，连接OM，

∵AP∥平面BDE，AP∥OM，

∵O是AC中点，∴M是PC中点

过P作PN∥DE，交CG于点N，

则N是GE中点，E是CN中点，∴＝2.