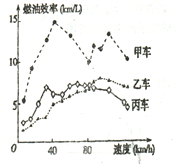
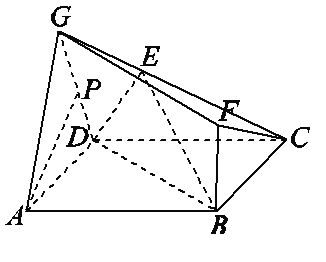
题目内容
【题目】已知一个动圆与两个定圆![]() 和
和![]() 均相切,其圆心的轨迹为曲线C.
均相切,其圆心的轨迹为曲线C.
(1) 求曲线C的方程;
(2) 过点F(![]() )做两条可相垂直的直线
)做两条可相垂直的直线![]() ,设
,设![]() 与曲线C交于A,B两点,
与曲线C交于A,B两点, ![]() 与曲线 C交于C,D两点,线段AC,BD分别与直线
与曲线 C交于C,D两点,线段AC,BD分别与直线![]() 交于M,M,N两点。求证|MF|:|NF|为定值.
交于M,M,N两点。求证|MF|:|NF|为定值.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析:(1)设动圆圆心为![]() ,半径为
,半径为![]() ,根据题设条件可得
,根据题设条件可得![]() ,
, ![]() ,
, ![]() ,再结合椭圆的第一定义即可得出曲线
,再结合椭圆的第一定义即可得出曲线![]() 的方程;(2)分别讨论
的方程;(2)分别讨论![]() ,
, ![]() 是否平行于坐标轴,当不平行于坐标轴时,设出
是否平行于坐标轴,当不平行于坐标轴时,设出![]() ,
, ![]() ,将方程代入到曲线
,将方程代入到曲线![]() 的方程,结合韦达定理,求出
的方程,结合韦达定理,求出![]() ,
, ![]() 点的坐标,即可求出
点的坐标,即可求出![]() 为定值.
为定值.
试题解析:(1)设动圆圆心为![]() ,半径为
,半径为![]()
∵两个定圆为![]() 和
和![]()
∴其圆心分别为![]() ,
, ![]() ,半径分别为
,半径分别为![]() ,
, ![]()
∵![]()
∴两个定圆相内含
∵动圆![]() 与两个圆均相切
与两个圆均相切
∴![]() ,
, ![]()
∴![]()
∴动点![]() 的轨迹为以
的轨迹为以![]() ,
, ![]() 为焦点,以4为长轴长的椭圆
为焦点,以4为长轴长的椭圆
∴曲线![]() 的方程为
的方程为![]()
(2)当![]() ,
, ![]() 平行于坐标轴时,可知
平行于坐标轴时,可知![]()
当![]() ,
, ![]() 不平行于坐标轴时,设
不平行于坐标轴时,设![]() ,
, ![]()
将![]() 的方程代入曲线
的方程代入曲线![]() 的方程中消去
的方程中消去![]() 化简得:
化简得: ![]()
∴![]() ,
, ![]()
同理可得![]() ,
, ![]()
由直线![]() 中令
中令![]() 可得
可得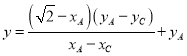 ①
①
∵![]() 与曲线
与曲线![]() 交于
交于![]() ,
, ![]() 两点,
两点, ![]() 与曲线
与曲线![]() 交于
交于![]() ,
, ![]() 两点
两点
∴![]() ,
, ![]() 代入①式化简得
代入①式化简得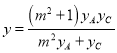
∴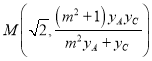
同理可得
∵![]()
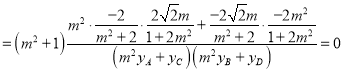
∴![]()
综上所述, ![]()

练习册系列答案
相关题目