Question

【题目】已知抛物线T的焦点为F，准线为l，过F的直线m与T交于A，B两点，C，D分别为A，B在l上的射影，M为AB的中点，若m与l不平行，则△CMD是(　　)

A. 等腰三角形且为锐角三角形

B. 等腰三角形且为钝角三角形

C. 等腰直角三角形

D. 非等腰的直角三角形

Answer 1

【答案】A

【解析】不妨设抛物线T的方程为y2＝2px(p>0).∵点A在抛物线y2＝2px上，F为抛物线的焦点，C，D分别为A，B在l上的射影，M为AB的中点，NM是M到抛物线准线的垂线，垂足为N，准线与x轴的交点为E，如图：

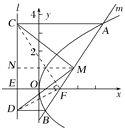
∴△CMD中，|CN|＝|ND|，所以△CMD是等腰三角形，

又根据抛物线定义，|AC|＝|AF|，|BD|＝|BF|，

∴∠CFD＝∠CFE＋∠DFE＝∠ACF＋∠BDF＝∠AFC＋∠BFD.

可得∠CFD＝90°，又|MN|>|EF|，可得∠CMD<90°.

则△CMD是等腰三角形且为锐角三角形.

答案　A