题目内容
【题目】函数g(x)=f(x)+2x,x∈R为奇函数.
(1)判断函数f(x)的奇偶性;
(2)若x>0时,f(x)=log3x,求函数g(x)的解析式.
【答案】
(1)解:任给x∈R,f(x)=g(x)﹣2xf(﹣x)=g(﹣x)+2x…(2分)
因为g(x)为奇函数,所以g(﹣x)=﹣g(x),
所以f(﹣x)=﹣g(x)+2x=﹣f(x),
所以f(x)为奇函数
(2)解:当x>0时,g(x)=log3x+2x
当x<0时,﹣x>0,所以g(﹣x)=log3(﹣x)﹣2x
因为 g(x)为奇函数
所以 g(x)=﹣g(﹣x)=﹣[log3(﹣x)﹣2x]=2x﹣log3(﹣x)
又因为奇函数g(0)=0
所以g(x)= 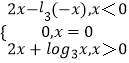
【解析】(1)函数g(x)=f(x)+2x(x∈R)为奇函数,g(﹣x)=f(﹣x)﹣2x=﹣g(x)=﹣f(x)﹣2x,可得f(﹣x)=﹣f(x),即可判断函数f(x)的奇偶性;(2)若x>0时,f(x)=log3x,求出x<0,x=0时的解析式,即可求函数g(x)的解析式.
【考点精析】认真审题,首先需要了解奇偶性与单调性的综合(奇函数在关于原点对称的区间上有相同的单调性;偶函数在关于原点对称的区间上有相反的单调性).

练习册系列答案
相关题目