Question

【题目】已知函数f（x）=2﹣ （x＞0），若存在实数m、n（m＜n）使f（x）在区间（m，n）上的值域为（tm，tn），则实数t的取值范围是 ．

Answer 1

【答案】（0，1）
【解析】解：画出函数f（x）的草图，如图示：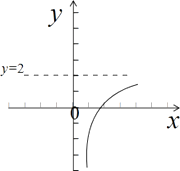
，
∴函数f（x）在（0，+∞）上单调递增，
∴2﹣ =tm，2﹣ =tn，
∴m，n是方程2﹣ =tx①的2个根，（0＜m＜n）
整理①得：tx2﹣2x+1=0，
∴ ，解得：0＜t＜1，
所以答案是：（0，1）．
【考点精析】解答此题的关键在于理解函数的值域的相关知识，掌握求函数值域的方法和求函数最值的常用方法基本上是相同的．事实上，如果在函数的值域中存在一个最小（大）数，这个数就是函数的最小（大）值．因此求函数的最值与值域，其实质是相同的．