题目内容
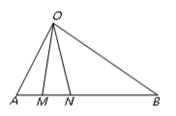
【题目】如图所示,某公路![]() 一侧有一块空地
一侧有一块空地![]() ,其中
,其中 ![]() ,
,![]() .当地政府拟在中间开挖一个人工湖△OMN,其中M,N都在边AB上(M,N不与A,B重合,M在A,N之间),且∠MON=30°.
.当地政府拟在中间开挖一个人工湖△OMN,其中M,N都在边AB上(M,N不与A,B重合,M在A,N之间),且∠MON=30°.
(1)若M在距离A点2 km处,求点M,N之间的距离;
(2)为节省投入资金,人工湖△OMN的面积要尽可能小.试确定M的位置,使△OMN的面积最小,并求出最小面积.
【答案】(1)![]() (2)最小面积是
(2)最小面积是![]()
【解析】试题分析:
(1)先利用余弦定理分别求出![]() ,再利用角度转化和正弦定理求出
,再利用角度转化和正弦定理求出![]() ;(2)设
;(2)设![]() ,利用三角形之间的正余弦定理转化应用,解得
,利用三角形之间的正余弦定理转化应用,解得![]() ,应用函数化简技巧,解得最小值
,应用函数化简技巧,解得最小值![]() 。
。
试题解析:
(1)在△OAB中,因为OA=3,OB=3![]() ,∠AOB=90°,所以∠OAB=60°.
,∠AOB=90°,所以∠OAB=60°.
在△OAM中,由余弦定理得OM2=AO2+AM2-2AO·AM·cosA=7,
所以OM=![]() ,所以cos∠AOM=
,所以cos∠AOM=![]() =
=![]() ,
,
在△OAN中,sin∠ONA=sin(∠A+∠AON)= sin(∠AOM+90°)=cos∠AOM=![]() .
.
在△OMN中,由![]() =
=![]() ,得MN=
,得MN=![]() ×
×![]() =
=![]() .
.
(2)解法1:设AM=x,0<x<3.
在△OAM中,由余弦定理得OM2=AO2+AM2-2AO·AM·cosA=x2-3x+9,
所以OM=![]() ,所以cos∠AOM=
,所以cos∠AOM=![]() =
=![]() ,
,
在△OAN中,sin∠ONA=sin(∠A+∠AON)= sin(∠AOM+90°)
=cos∠AOM=![]() .
.
由![]() =
=![]() ,得ON=
,得ON=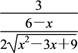 ·
·![]() =
=![]() .
.
所以S△OMN=![]() OM·ON·sin∠MON=
OM·ON·sin∠MON=![]() ·
·![]() ·
·![]() ·
·![]()
=![]() ,0<x<3.
,0<x<3.
令6-x=t,则x=6-t,3<t<6,则S△OMN=![]() =
=![]() (t-9+
(t-9+![]() )
)
≥![]() ·(2
·(2![]() -9)=
-9)=![]() .
.
当且仅当t=![]() ,即t=3
,即t=3![]() ,x=6-3
,x=6-3![]() 时等号成立,S△OMN的最小值为
时等号成立,S△OMN的最小值为![]() .
.
所以M的位置为距离A点6-3![]() km处,可使△OMN的面积最小,最小面积是
km处,可使△OMN的面积最小,最小面积是
![]() km2.
km2.
解法2:设∠AOM=θ,0<θ<![]()
在△OAM中,由![]() =
=![]() ,得OM=
,得OM=![]() .
.
在△OAN中,由![]() =
=![]() ,得ON=
,得ON=![]() =
=![]() .
.
所以S△OMN=![]() OM·ON·sin∠MON=
OM·ON·sin∠MON=![]() ·
·![]() ·
·![]() ·
·![]()
=![]() =
=![]() =
=![]()
=![]() =
=![]() ,0<θ<
,0<θ<![]() .
.
当2θ+![]() =
=![]() ,即θ=
,即θ=![]() 时,S△OMN的最小值为
时,S△OMN的最小值为![]() .
.
所以应设计∠AOM=![]() ,可使△OMN的面积最小,最小面积是
,可使△OMN的面积最小,最小面积是![]() km2.
km2.