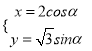Question

【题目】在平面直角坐标系xOy中，经过点 且斜率为k的直线l与椭圆 有两个不同的交点P和Q．
（Ⅰ）求k的取值范围；
（Ⅱ）设椭圆与x轴正半轴、y轴正半轴的交点分别为A，B，是否存在常数k，使得向量 与 共线？如果存在，求k值；如果不存在，请说明理由．

Answer 1

【答案】解：（Ⅰ）由已知条件，直线l的方程为 ，
代入椭圆方程得 ．
整理得 ①
直线l与椭圆有两个不同的交点P和Q，等价于①的判别式△= ，
解得 或 ．即k的取值范围为 ．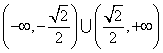
（Ⅱ）设P（x1 ， y1），Q（x2 ， y2），则 ，
由方程①， ． ②
又 ． ③
而 ．
所以 与 共线等价于 ，
将②③代入上式，解得 ．
由（Ⅰ）知 或 ，
故没有符合题意的常数k
【解析】（1）直线l与椭圆有两个不同的交点，即方程组有2个不同解，转化为判别式大于0．（2）利用2个向量共线时，坐标之间的关系，由一元二次方程根与系数的关系求两根之和，解方程求常数k．
【考点精析】关于本题考查的向量的共线定理和平面的概念、画法及表示，需要了解设，，其中，则当且仅当时，向量、共线；经过不在同一条直线上的三点确定一个面;平面的画法：水平放置的平面通常画成一个平行四边形，锐角画成450，且横边画成邻边的2倍长才能得出正确答案．