Question

【题目】已知是椭圆上的两点.

（1）求椭圆的离心率；

（2）已知直线过点，且与椭圆交于另一点（不同于点），若以为直径的圆经过点，求直线的方程.

Answer 1

【答案】（1）（2）

【解析】

（1）将A和B点的坐标代入椭圆G的方程，列出方程组求出的值，再求出和离心率；
（2）由（1）求出椭圆G的方程，对直线的斜率进行讨论，不妨设直线的方程，与椭圆G的方程联立后，利用韦达定理写出式子，将条件转化为，由向量数量积的坐标运算列出式子，代入化简后求出的值，即得直线的方程.

解：（1）由已知，

由点在椭圆上可得，

解得.

所以，

所以椭圆的离心率是；

（2）当直线过点且斜率不存在时，可得点，不满足条件；

设直线的方程为），点，

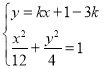由可得，

显然，此方程两个根是点和点的橫坐标，

所以，即，

所以，

因为以为直径的圆经过点，

所以，即，

，

即，

，，

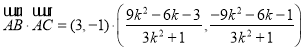
当时，即直线，与已知点不同于点矛盾，

所以，

所以直线的方程为.