题目内容
【题目】已知双曲线
的左、右焦点分别为
，实轴长为4，渐近线方程为
，点N在圆
上，则
的最小值为( )
A. 
B. 5C. 6D. 7
【答案】B
【解析】
求得双曲线的a，b，可得双曲线方程，求得焦点坐标，运用双曲线的定义和三点共线取得最小值，连接CF2，交双曲线于M，圆于N，计算可得所求最小值．
由题意可得2a＝4，即a＝2，
渐近线方程为y＝±
x，即有
，
即b＝1，可得双曲线方程为
y2＝1，
焦点为F1（
，0），F2，（
，0），
由双曲线的定义可得|MF1|＝2a+|MF2|＝4+|MF2|，
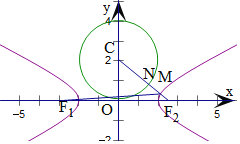
由圆x2+y2﹣4y＝0可得圆心C（0，2），半径r＝2，
|MN|+|MF1|＝4+|MN|+|MF2|，
连接CF2，交双曲线于M，圆于N，
可得|MN|+|MF2|取得最小值，且为|CF2|
3，
则则|MN|+|MF1|的最小值为4+3﹣2＝5．
故选：B．
练习册系列答案
相关题目
