题目内容
定义在R上的函数f(x)满足f(-x)=-f(x),f(x-2)=f(x+2),且x∈(-1,0)时,f(x)=2x+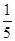 ,则f(log220)的值为( )
,则f(log220)的值为( )
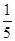 ,则f(log220)的值为( )
,则f(log220)的值为( )| A.1 | B. | C.-1 | D.- |
C
由f(-x)=-f(x),f(x-2)=f(x+2),可知函数为奇函数,且f(x+4)=f(x),∴函数的周期为4.∵4<log220<5,0<log220-4<1,即log220-4=log2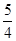 ,
,
∴f(log220)=f(log220-4)=f(log2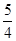 )
)
=-f(-log2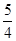 ),∵-1<log2
),∵-1<log2 <0,∴f(log2
<0,∴f(log2 )=
)=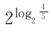 +
+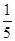 =
= +
+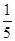 =1,∴f(log220)=f(log220-4)=-f(log2
=1,∴f(log220)=f(log220-4)=-f(log2 )=-1,选C.
)=-1,选C.
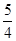 ,
,∴f(log220)=f(log220-4)=f(log2
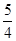 )
)=-f(-log2
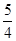 ),∵-1<log2
),∵-1<log2 <0,∴f(log2
<0,∴f(log2 )=
)=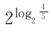 +
+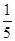 =
= +
+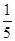 =1,∴f(log220)=f(log220-4)=-f(log2
=1,∴f(log220)=f(log220-4)=-f(log2 )=-1,选C.
)=-1,选C.
练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
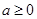 ,函数
,函数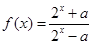
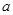 =4,求函数
=4,求函数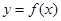 的反函数
的反函数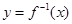 ;
; (ex+e﹣x)
(ex+e﹣x)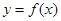 的图象与函数
的图象与函数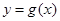 的图象关于直线
的图象关于直线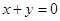 对称,则
对称,则
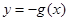
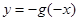
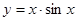 ;②
;②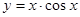 ;③
;③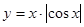 ; ④
; ④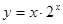 的图象(部分)如下,但顺序被打乱,则按照从左到右的顺序对应的函数序号是( )
的图象(部分)如下,但顺序被打乱,则按照从左到右的顺序对应的函数序号是( )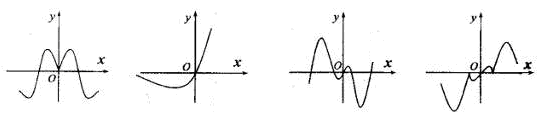
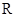 上的偶函数
上的偶函数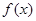 满足
满足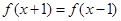 ,且当
,且当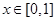 时,
时,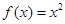 ,则关于
,则关于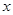 的方程
的方程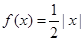 在
在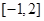 上根的个数是( )
上根的个数是( )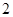
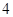

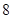
 ,若
,若 是奇函数,则
是奇函数,则 的值是 .
的值是 .