题目内容
设函数f(x)=x|x|+bx+c,给出下列四个命题:
①c=0时,y=f(x)是奇函数;
②b=0,c>0时,方程f(x)=0只有一个实数根;
③y=f(x)的图象关于点(0,c)对称;
④方程f(x)=0最多有两个实根.
其中正确的命题是( )
①c=0时,y=f(x)是奇函数;
②b=0,c>0时,方程f(x)=0只有一个实数根;
③y=f(x)的图象关于点(0,c)对称;
④方程f(x)=0最多有两个实根.
其中正确的命题是( )
| A.①② | B.②④ | C.①②③ | D.①②④ |
C
当c=0时,f(x)=x|x|+bx,
此时f(-x)=-f(x),故f(x)为奇函数.①正确;
当b=0,c>0时,f(x)=x|x|+c,
若x≥0,f(x)=0无解,若x<0,
f(x)=0有一解x=-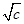 ,②正确;
,②正确;
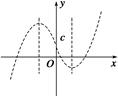
结合图象知③正确,④不正确.
此时f(-x)=-f(x),故f(x)为奇函数.①正确;
当b=0,c>0时,f(x)=x|x|+c,
若x≥0,f(x)=0无解,若x<0,
f(x)=0有一解x=-
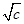 ,②正确;
,②正确;结合图象知③正确,④不正确.


练习册系列答案
相关题目
 ,函数
,函数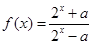
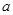 =4,求函数
=4,求函数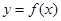 的反函数
的反函数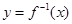 ;
; (ex+e﹣x)
(ex+e﹣x)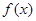 满足
满足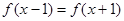 ,且在
,且在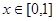 时,
时,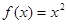 ,则关于
,则关于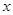 的方程
的方程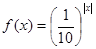 在
在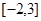 上的根的个数是
上的根的个数是 ,则f(﹣1)=( )
,则f(﹣1)=( ) 上的偶函数
上的偶函数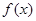 满足
满足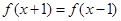 ,且当
,且当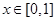 时,
时,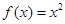 ,则关于
,则关于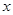 的方程
的方程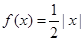 在
在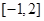 上根的个数是( )
上根的个数是( )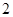
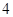

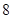
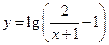 的图象关于( )
的图象关于( )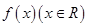 是奇函数,函数
是奇函数,函数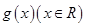 是偶函数,则一定成立的是( )
是偶函数,则一定成立的是( )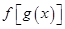 是奇函数
是奇函数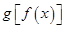 是奇函数
是奇函数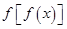 是奇函数
是奇函数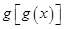 是奇函数
是奇函数