题目内容
5．已知θ∈（π，$\frac{3}{2}$π），且sin$\frac{θ}{2}$=$\frac{4}{5}$，求$\frac{sinθ}{1+cosθ}$的值．分析 利用同角三角函数的基本关系式求出半角的余弦函数，利用二倍角公式求解即可．
解答 解：θ∈（π，$\frac{3}{2}$π），且sin$\frac{θ}{2}$=$\frac{4}{5}$，
∴cos$\frac{θ}{2}$=$-\frac{3}{5}$，
∴sinθ=2×$\frac{4}{5}×（-\frac{3}{5}）$=-$\frac{24}{25}$，
cosθ=1-2sin2θ=1-2×$（{\frac{4}{5}）}^{2}$=-$\frac{7}{25}$．
$\frac{sinθ}{1+cosθ}$=$\frac{-\frac{24}{25}}{1-\frac{7}{25}}$=$-\frac{4}{3}$．
点评 本题考查同角三角函数的基本关系式，二倍角公式的应用，考查计算能力．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
13．
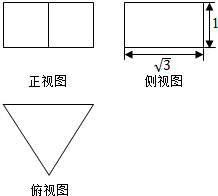若正三棱柱（底面为正三角形，且侧棱与底面垂直的三棱柱）的三视图如图所示，该三棱柱的表面积是（ ）
若正三棱柱（底面为正三角形，且侧棱与底面垂直的三棱柱）的三视图如图所示，该三棱柱的表面积是（ ）| A． | $\sqrt{3}$ | B． | 6+2$\sqrt{3}$ | C． | 6+$\sqrt{3}$ | D． | $\frac{9\sqrt{3}}{2}$ |
10．甲、乙、丙三人独立地去译一个密码，分别译出的概率为$\frac{1}{5}$，$\frac{1}{3}$，$\frac{1}{4}$，则此密码能译出的概率是（ ）
| A． | $\frac{1}{60}$ | B． | $\frac{2}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{59}{60}$ |