题目内容
定义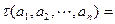
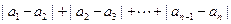 为有限项数列
为有限项数列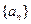 的波动强度.
的波动强度.
(Ⅰ)当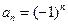 时,求
时,求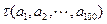 ;
;
(Ⅱ)若数列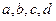 满足
满足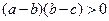 ,求证:
,求证: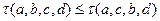 ;
;
(Ⅲ)设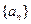 各项均不相等,且交换数列
各项均不相等,且交换数列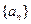 中任何相邻两项的位置,都会使数列的波动强度增加,求证:数列
中任何相邻两项的位置,都会使数列的波动强度增加,求证:数列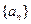 一定是递增数列或递减数列
一定是递增数列或递减数列
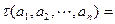
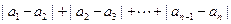 为有限项数列
为有限项数列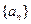 的波动强度.
的波动强度.(Ⅰ)当
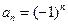 时,求
时,求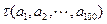 ;
;(Ⅱ)若数列
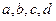 满足
满足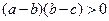 ,求证:
,求证: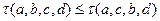 ;
;(Ⅲ)设
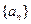 各项均不相等,且交换数列
各项均不相等,且交换数列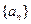 中任何相邻两项的位置,都会使数列的波动强度增加,求证:数列
中任何相邻两项的位置,都会使数列的波动强度增加,求证:数列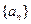 一定是递增数列或递减数列
一定是递增数列或递减数列(Ⅰ)解: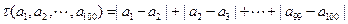 ………………1分
………………1分
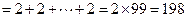 . ………………3分
. ………………3分
(Ⅱ)证明:因为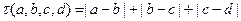 ,
,
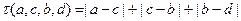 ,
,
所以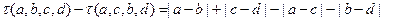 . ……………4分
. ……………4分
因为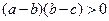 ,所以
,所以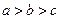 ,或
,或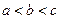 .
.
若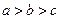 ,则
,则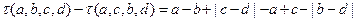
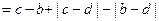
当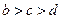 时,上式
时,上式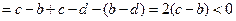 ,
,
当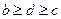 时,上式
时,上式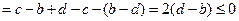 ,
,
当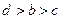 时,上式
时,上式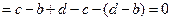 ,
,
即当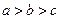 时,
时,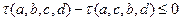 . ……………………6分
. ……………………6分
若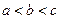 ,
,
则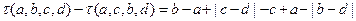 ,
,
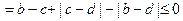 .(同前)
.(同前)
所以,当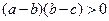 时,
时,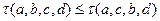 成立. …………………7分
成立. …………………7分
(Ⅲ)证明:由(Ⅱ)易知对于四个数的数列,若第三项的值介于前两项的值之间,则交换第二项与第三项的位置将使数列波动强度减小或不变.(将此作为引理)
下面来证明当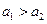 时,
时,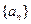 为递减数列.
为递减数列.
(ⅰ)证明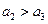 .
.
若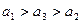 ,则由引理知交换
,则由引理知交换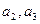 的位置将使波动强度减小或不变,与已知矛盾.
的位置将使波动强度减小或不变,与已知矛盾.
若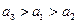 ,则
,则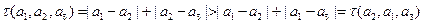 ,与已知矛盾.
,与已知矛盾.
所以,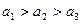 . ………………………9分
. ………………………9分
(ⅱ)设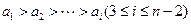 ,证明
,证明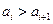 .
.
若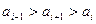 ,则由引理知交换
,则由引理知交换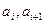 的位置将使波动强度减小或不变,与已知矛盾.
的位置将使波动强度减小或不变,与已知矛盾.
若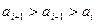 ,则
,则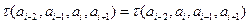 ,与已知矛盾.
,与已知矛盾.
所以,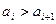 . …………………11分
. …………………11分
(ⅲ)设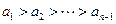 ,证明
,证明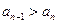 .
.
若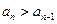 ,考查数列
,考查数列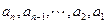 ,
,
则由前面推理可得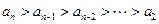 ,与
,与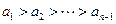 矛盾.
矛盾.
所以,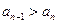 . …………………12分
. …………………12分
综上,得证.
同理可证:当 时,有
时,有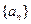 为递增数列. ……………………13分
为递增数列. ……………………13分
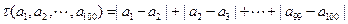 ………………1分
………………1分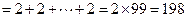 . ………………3分
. ………………3分(Ⅱ)证明:因为
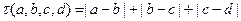 ,
,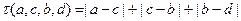 ,
,所以
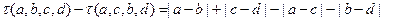 . ……………4分
. ……………4分因为
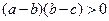 ,所以
,所以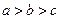 ,或
,或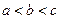 .
.若
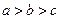 ,则
,则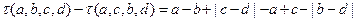
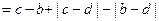
当
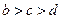 时,上式
时,上式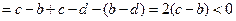 ,
,当
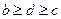 时,上式
时,上式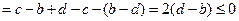 ,
,当
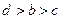 时,上式
时,上式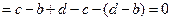 ,
,即当
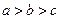 时,
时,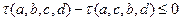 . ……………………6分
. ……………………6分若
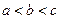 ,
,则
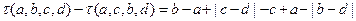 ,
,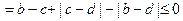 .(同前)
.(同前)所以,当
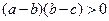 时,
时,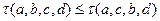 成立. …………………7分
成立. …………………7分(Ⅲ)证明:由(Ⅱ)易知对于四个数的数列,若第三项的值介于前两项的值之间,则交换第二项与第三项的位置将使数列波动强度减小或不变.(将此作为引理)
下面来证明当
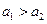 时,
时,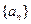 为递减数列.
为递减数列.(ⅰ)证明
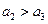 .
.若
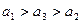 ,则由引理知交换
,则由引理知交换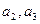 的位置将使波动强度减小或不变,与已知矛盾.
的位置将使波动强度减小或不变,与已知矛盾.若
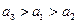 ,则
,则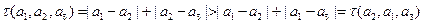 ,与已知矛盾.
,与已知矛盾.所以,
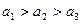 . ………………………9分
. ………………………9分(ⅱ)设
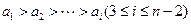 ,证明
,证明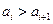 .
.若
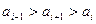 ,则由引理知交换
,则由引理知交换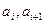 的位置将使波动强度减小或不变,与已知矛盾.
的位置将使波动强度减小或不变,与已知矛盾.若
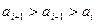 ,则
,则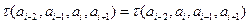 ,与已知矛盾.
,与已知矛盾.所以,
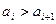 . …………………11分
. …………………11分(ⅲ)设
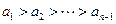 ,证明
,证明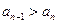 .
.若
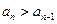 ,考查数列
,考查数列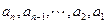 ,
,则由前面推理可得
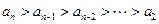 ,与
,与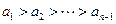 矛盾.
矛盾.所以,
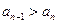 . …………………12分
. …………………12分综上,得证.
同理可证:当
 时,有
时,有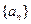 为递增数列. ……………………13分
为递增数列. ……………………13分略

练习册系列答案
相关题目
 中,
中, ,则
,则



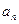 }的前6项和为60,且
}的前6项和为60,且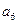 为
为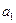 和
和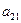 的等比中项.
的等比中项.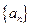
 的通项公式;
的通项公式; 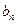 }满足
}满足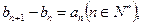 且
且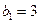 ,求数列{
,求数列{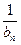 }的前n项和
}的前n项和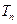 .
.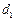 和
和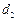 为公差的等差数列
为公差的等差数列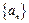 和
和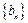 满足
满足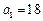 ,
, 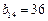 ,
,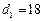 ,
, 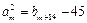 ,求
,求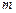 的取值范围;
的取值范围;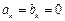 ,且数列
,且数列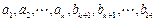 …的前
…的前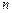 项和
项和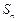 满足
满足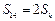 ,
,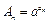 ,
,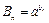 ,
, 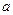 >0且
>0且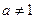 ,探究不等式
,探究不等式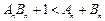 是否对一切正整数
是否对一切正整数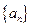 的前
的前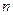 项和为
项和为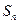 ,若
,若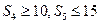 ,则
,则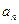 的最大值为___________.
的最大值为___________.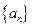 中,
中,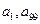 是函数
是函数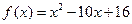 的两个零点,则
的两个零点,则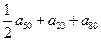 ( )
( )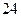
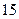

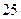
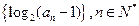 为等差数列,且
为等差数列,且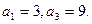
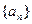 的通项公式;
的通项公式; 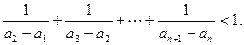
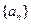 ,
,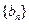 中已知
中已知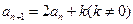 ,
,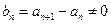
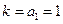 ,求数列
,求数列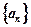 中,已知
中,已知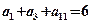 ,那么
,那么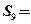 ( )
( ) 8
8