题目内容
(本小题满分16分)
已知分别以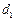 和
和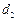 为公差的等差数列
为公差的等差数列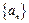 和
和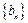 满足
满足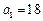 ,
, 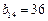 ,
,
(1)若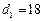 ,
, 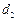 ≥2917,且
≥2917,且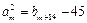 ,求
,求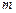 的取值范围;
的取值范围;
(2)若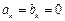 ,且数列
,且数列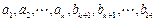 …的前
…的前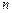 项和
项和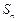 满足
满足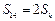 ,
,
①求数列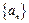 和
和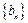 的通项公式;
的通项公式;
②令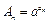 ,
,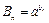 ,
, 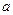 >0且
>0且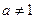 ,探究不等式
,探究不等式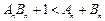 是否对一切正整数
是否对一切正整数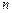 恒成立?
恒成立?
已知分别以
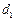 和
和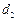 为公差的等差数列
为公差的等差数列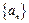 和
和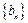 满足
满足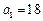 ,
, 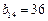 ,
,(1)若
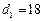 ,
, 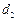 ≥2917,且
≥2917,且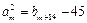 ,求
,求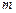 的取值范围;
的取值范围;(2)若
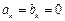 ,且数列
,且数列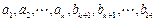 …的前
…的前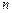 项和
项和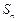 满足
满足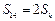 ,
,①求数列
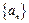 和
和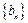 的通项公式;
的通项公式;②令
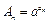 ,
,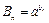 ,
, 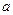 >0且
>0且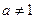 ,探究不等式
,探究不等式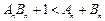 是否对一切正整数
是否对一切正整数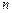 恒成立?
恒成立? (1)因为等差数列
(1)因为等差数列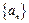 中,
中,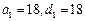 ,所以
,所以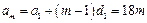 ,
,因为等差数列
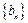 中,
中,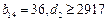 ,所以
,所以 ,……………………2分
,……………………2分又因为
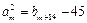 ,所以
,所以 ,故有
,故有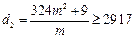 ,
,因为
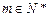 ,所以
,所以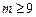 ; …………………………………………………………………………4分
; …………………………………………………………………………4分(2)①因为
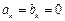 ,所以
,所以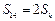 ,即
,即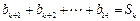 ,
,亦即
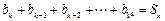 ,所以有
,所以有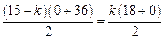 ,解得
,解得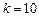 ,…6分
,…6分由
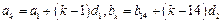 知,
知,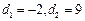 , ……………………………………8分
, ……………………………………8分所以
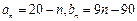 ; ………………………………………………………………………10分
; ………………………………………………………………………10分②因为
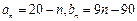 ,所以
,所以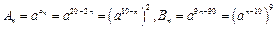 ,
,又
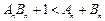 等价于
等价于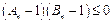 ,且
,且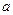 >0且
>0且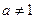 ,
,当
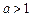 时,若
时,若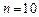 时,
时,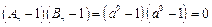 ,
,若
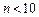 时,
时,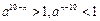 ,所以
,所以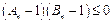 成立,
成立,若
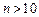 时,
时,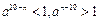 ,所以
,所以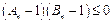 成立,
成立,所以当
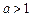 时,对任意
时,对任意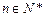 ,所以
,所以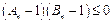 成立. …………………………………14分
成立. …………………………………14分同理可证,当
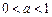 时,对任意
时,对任意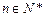 ,所以
,所以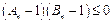 成立.
成立.即当
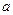 >0且
>0且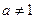 时,对任意
时,对任意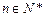 ,所以
,所以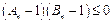 成立.……………………………16分
成立.……………………………16分略

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
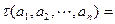
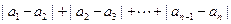 为有限项数列
为有限项数列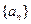 的波动强度.
的波动强度.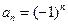 时,求
时,求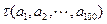 ;
;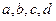 满足
满足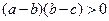 ,求证:
,求证: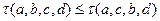 ;
;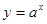 的图象过点
的图象过点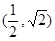 ,如果点
,如果点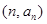
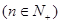 在函数
在函数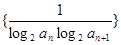 的前
的前 项和为 ( )
项和为 ( )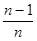
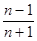
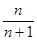
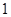
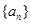 满足
满足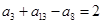 ,则
,则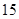 项和
项和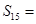
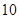
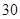
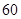
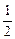 .
.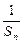 }是等差数列;
}是等差数列;
 成等差数列,且
成等差数列,且 ,则
,则 =
= 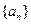 满足
满足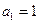 ,
,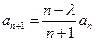 ,其中
,其中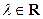 ,
,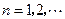 .给出下列命题:
.给出下列命题: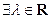 ,对于任意
,对于任意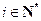 ,
,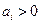 ;
;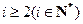 ,
,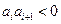 ;
;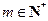 ,当
,当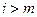 (
(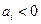 .
.