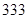题目内容
在直角三角形ABC中,斜边BC为10,以BC中点为圆心,作半径为3的圆,分别交BC于P、Q两点,设L=|AP|2+|AQ|2+|PQ|2,试问L是否为定值?如果是定值,求出定值,反之说明理由.
根据题意,可得|OP|=|OQ|=3.
∵O为Rt△ABC的斜边中点,∴|OA|=
|BC|=5,
 在△AOP中,根据余弦定理,
在△AOP中,根据余弦定理,
可得|AP|2=|OA|2+|OP|2-2|OA|•|OP|cos∠AOP…①.
同理在△AOQ中,|AQ|2=|OA|2+|OQ|2-2|OA|•|OQ|cos∠AOQ…②.
∵∠AOP+∠AOQ=180°,可得cos∠AOP+cos∠AOQ=0
∴将①、②相加,可得|AP|2+|AQ|2=2(|OA|2+|OP|2)=2(25+9)=68
又∵|PQ|2=4|OP|2=36,
∴L=|AP|2+|AQ|2+|PQ|2=68+36=104,即L为定值.
∵O为Rt△ABC的斜边中点,∴|OA|=
| 1 |
| 2 |
 在△AOP中,根据余弦定理,
在△AOP中,根据余弦定理,可得|AP|2=|OA|2+|OP|2-2|OA|•|OP|cos∠AOP…①.
同理在△AOQ中,|AQ|2=|OA|2+|OQ|2-2|OA|•|OQ|cos∠AOQ…②.
∵∠AOP+∠AOQ=180°,可得cos∠AOP+cos∠AOQ=0
∴将①、②相加,可得|AP|2+|AQ|2=2(|OA|2+|OP|2)=2(25+9)=68
又∵|PQ|2=4|OP|2=36,
∴L=|AP|2+|AQ|2+|PQ|2=68+36=104,即L为定值.

练习册系列答案
相关题目
 是数列
是数列 中的第( )项.
中的第( )项.