题目内容
在△ABC中，BC=
，AC=3，sinC=2sinA．
（1）求边长AB的值；
（2）求△ABC的面积．
| 5 |
（1）求边长AB的值；
（2）求△ABC的面积．
（1）∵BC=
，AC=3，sinC=2sinA，
∴由正弦定理
=
得：AB=
=
=2BC=2
；
（2）∵BC=
，AC=3，AB=2
，
∴由余弦定理cosC=
=
=-
，
∵C为三角形内角，
∴sinC=
=
，
则S△ABC=
AC•BCsinC=
×3×
×
=3．
| 5 |
∴由正弦定理
| AB |
| sinC |
| BC |
| sinA |
| BCsinC |
| sinA |
| 2BCsinA |
| sinA |
| 5 |
（2）∵BC=
| 5 |
| 5 |
∴由余弦定理cosC=
| AC2+BC2-AB2 |
| 2AC•BC |
| 9+5-20 | ||
6
|
| ||
| 5 |
∵C为三角形内角，
∴sinC=
| 1-cos2C |
2
| ||
| 5 |
则S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
2
| ||
| 5 |
练习册系列答案
口算能手系列答案
相关题目
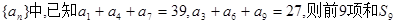的值为（ ）