题目内容
△ABC中,已知其面积为S=
(a2+b2-c2),则角C的度数为( )
| 1 |
| 4 |
| A.135° | B.45° | C.60° | D.120° |
∵cosC=
,即a2+b2-c2=2abcosC,S=
absinC,且S=
(a2+b2-c2),
∴
absinC=
abcosC,即tanC=1,
∵C为三角形的内角,
∴C=45°.
故选B
| a2+b2-c2 |
| 2ab |
| 1 |
| 2 |
| 1 |
| 4 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
∵C为三角形的内角,
∴C=45°.
故选B

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目




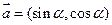 ,
,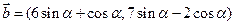 ,设函数
,设函数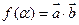 .
.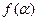 的最大值;
的最大值;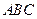 中,角
中,角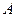 、
、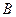 、
、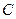 的对边分别为
的对边分别为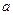 、
、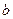 、
、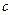 ,
,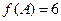 ,且
,且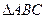 的面积为3,
的面积为3,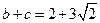 ,求
,求