题目内容
设△ABC的内角A,B,C所对的边分别为a,b,c,若c(1+cosA)=
a•sinC
(1)求角A的大小;
(2)若a=2,△ABC的面积为
,求△ABC的周长.
| 3 |
(1)求角A的大小;
(2)若a=2,△ABC的面积为
| 3 |
(1)由已知及正弦定理得sinC(1+cosA)=
sinAsinC,
∵sinC≠0,∴1+cosA=
sinA,即
sinA-cosA=2(
sinA-
cosA)=2sin(A-
)=1,
∴A-
=
或A-
=
(舍去),
∴A=
;
(2)∵a=2,cosA=cos
=
,
由余弦定理得:a2=b2+c2-2bccosA,即b2+c2-bc=4,①
∵△ABC的面积为
,即
bcsinA=
bc=
,
∴bc=4,②
联立①②得:(b+c)2=4+3bc=16,
∴b+c=4,
则△ABC周长为a+b+c=2+4=6.
| 3 |
∵sinC≠0,∴1+cosA=
| 3 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
∴A-
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
∴A=
| π |
| 3 |
(2)∵a=2,cosA=cos
| π |
| 3 |
| 1 |
| 2 |
由余弦定理得:a2=b2+c2-2bccosA,即b2+c2-bc=4,①
∵△ABC的面积为
| 3 |
| 1 |
| 2 |
| ||
| 4 |
| 3 |
∴bc=4,②
联立①②得:(b+c)2=4+3bc=16,
∴b+c=4,
则△ABC周长为a+b+c=2+4=6.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
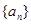 的前
的前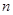 项和
项和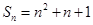 ,
,