题目内容
若直线4x-3y-2=0与圆x2+y2-2ax+4y+a2-12=0总有两个不同交点，则a的取值范围是
| A．-3＜a＜7 | B．-6＜a＜4 |
| C．-7＜a＜3 | D．-21＜a＜19 |
B
解：整理圆方程为（x-a）2+（y+2）2=16，
∴圆心坐标（a，-2），半径r=4
∵直线与圆总有两个交点，
∴圆心到直线的距离小于半径，那么解得-6＜a＜4，选B
∴圆心坐标（a，-2），半径r=4
∵直线与圆总有两个交点，
∴圆心到直线的距离小于半径，那么解得-6＜a＜4，选B
练习册系列答案
培优口算题卡系列答案
相关题目
与圆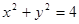
上任一点连线的中点轨迹方程是（ ）
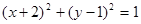
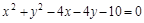上的点到直线
的最大距离是_________。
的切线
与
轴的正半轴、
轴的正半轴分别交于点
，当
取最小值时，切线
的动弦，且|BC|=6，则BC的中点的轨迹方程是 .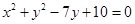
相交，所得公共弦平行于已知直线
，又圆C经过点A（-2，3），B（1，4），求圆C的方程。
＋
－4x－6y－12＝0上至少有三点到直线4x－3y＝m的距离是4，则m的取值范围是( )
表示的曲线为圆，则
的取值范围是（ ）
．
． 
