题目内容
已知圆C与圆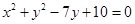
相交，所得公共弦平行于已知直线
，又圆C经过点A（-2，3），B（1，4），求圆C的方程。
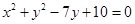相交，所得公共弦平行于已知直线 ，又圆C经过点A（-2，3），B（1，4），求圆C的方程。所求圆C的方程为
本试题主要是考查圆圆位置关系的运用，以及直线与圆的位置关系的运用。
由已知得圆C的弦AB的中点坐标，以及圆C的弦AB的垂直平分线方程，那么得到圆心的坐标，和两圆连心线所在直线的方程，那么可以解得。
解1：（利用公共弦所在直线的方程）：设圆C方程为
，
则圆C与已知圆的公共弦所在直线方程为
…………….. 4分
∴由题设得：
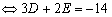①又点A、B在圆C上，故有： 
②
③……………………………… 7分
∴所求圆C的方程为：
……………………….………..10分
解2：（利用圆的性质）：由已知得圆C的弦AB的中点坐标为
，
∴圆C的弦AB的垂直平分线方程为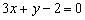
④
又已知圆圆心为
∴两圆连心线所在直线的方程为
⑤………….6分
设圆心C（a,b），则由④、⑤得
解之得 
而圆C的半径
∴所求圆C的方程为
………………………………………………10分
由已知得圆C的弦AB的中点坐标，以及圆C的弦AB的垂直平分线方程，那么得到圆心的坐标，和两圆连心线所在直线的方程，那么可以解得。
解1：（利用公共弦所在直线的方程）：设圆C方程为
，则圆C与已知圆的公共弦所在直线方程为
…………….. 4分∴由题设得：
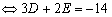①又点A、B在圆C上，故有： ② ③……………………………… 7分∴所求圆C的方程为：
……………………….………..10分解2：（利用圆的性质）：由已知得圆C的弦AB的中点坐标为
，∴圆C的弦AB的垂直平分线方程为
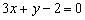④ 又已知圆圆心为
∴两圆连心线所在直线的方程为
⑤………….6分设圆心C（a,b），则由④、⑤得
解之得 而圆C的半径
∴所求圆C的方程为
………………………………………………10分
练习册系列答案
阶梯计算系列答案
相关题目
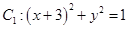，圆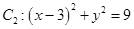
同时外切的动圆圆心的轨迹方程是_____________。
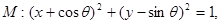直线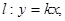
下面四个命题
和
直线
和圆
相切
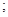
使得直线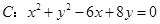
的圆心坐标为（ ）
轴切于点(5，0)并在y轴上截取弦长为10的圆的方程。
，点P是椭圆C：
上一点，过点P作圆O的两条切线PA、PB，A、B为切点，直线AB分别交
轴、
轴于点M、N，则
的面积的最小值是
B．1 C．
D．
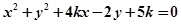表示圆，则
的取值范围是( )
Ｂ.
D.
表示圆心为C（2，2），半径为2的圆，则a、b、c的值依次为
、4、4；