题目内容
设函数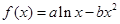 ,
,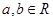
(1)若函数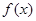 在
在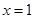 处与直线
处与直线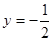 相切;
相切;
①求实数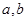 的值;②求函数
的值;②求函数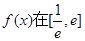 上的最大值;
上的最大值;
(2)当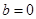 时,若不等式
时,若不等式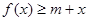 对所有的
对所有的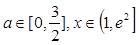 都成立,求实数
都成立,求实数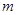 的取值范围.
的取值范围.
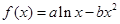 ,
,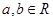
(1)若函数
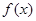 在
在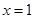 处与直线
处与直线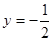 相切;
相切;①求实数
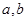 的值;②求函数
的值;②求函数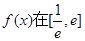 上的最大值;
上的最大值;(2)当
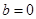 时,若不等式
时,若不等式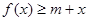 对所有的
对所有的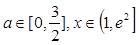 都成立,求实数
都成立,求实数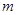 的取值范围.
的取值范围.解:(1)①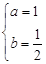 ②
②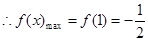
(2)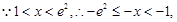
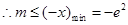
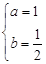 ②
②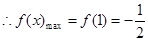
(2)
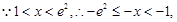
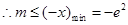
本试题主要是考查了导数在研究函数中的运用。
(1)因为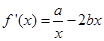 ∵函数
∵函数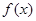 在
在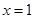 处与直线
处与直线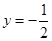 相切
相切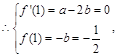 解得a,b的值。并且
解得a,b的值。并且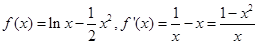 ,求导数的符号与函数单调性的关系得到最值。
,求导数的符号与函数单调性的关系得到最值。
(2)因为当b=0时,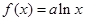 若不等式
若不等式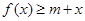 对所有的
对所有的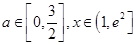 都成立,
都成立,
则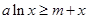 对所有的
对所有的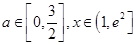 都成立,
都成立,
即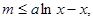 对所有的
对所有的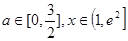 都成立转化与化归思想的运用。
都成立转化与化归思想的运用。
(1)因为
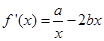 ∵函数
∵函数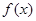 在
在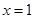 处与直线
处与直线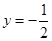 相切
相切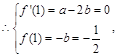 解得a,b的值。并且
解得a,b的值。并且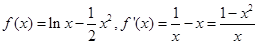 ,求导数的符号与函数单调性的关系得到最值。
,求导数的符号与函数单调性的关系得到最值。(2)因为当b=0时,
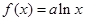 若不等式
若不等式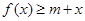 对所有的
对所有的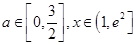 都成立,
都成立,则
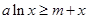 对所有的
对所有的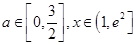 都成立,
都成立,即
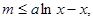 对所有的
对所有的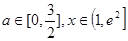 都成立转化与化归思想的运用。
都成立转化与化归思想的运用。
练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
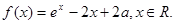
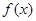 的单调区间与极值;
的单调区间与极值;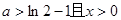 时,
时,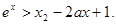
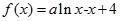 ,(
,(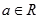 ),曲线
),曲线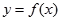 在点
在点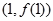 处的切线垂直于
处的切线垂直于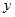 轴.
轴.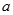 的值;
的值;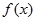 的极值.
的极值.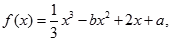
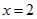 是
是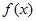 的一个极值点.
的一个极值点.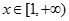 时,
时,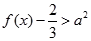 恒成立,求
恒成立,求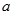 的取值范围。
的取值范围。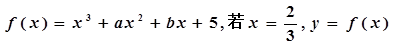 有极值,且曲线
有极值,且曲线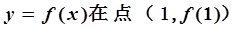 处的切线斜率为3.
处的切线斜率为3.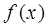 的解析式;
的解析式; 在[-4,1]上的最大值和最小值。
在[-4,1]上的最大值和最小值。 有三个零点,求实数
有三个零点,求实数 的取值范围.
的取值范围.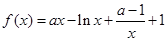 .
.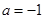 时,求曲线
时,求曲线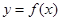 在点
在点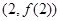 处的切线方程;
处的切线方程;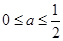 时,讨论
时,讨论 的单调性.
的单调性.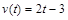 (
(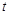 的单位:秒,
的单位:秒,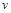 的单位:米/秒)的速度做变速直线运动,则该物体从时刻
的单位:米/秒)的速度做变速直线运动,则该物体从时刻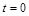 到5秒运动的路程
到5秒运动的路程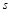 为 米.
为 米.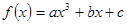 在点
在点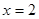 处取得极值
处取得极值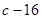 。
。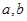 的值;
的值;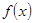 有极大值28,求
有极大值28,求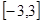 上的最小值。
上的最小值。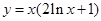 在点(1,1)处的切线方程是____________________
在点(1,1)处的切线方程是____________________