题目内容
(本小题满分12分)
设a为实数,函数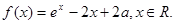
(I)求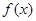 的单调区间与极值;
的单调区间与极值;
(II)求证:当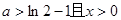 时,
时,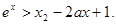
设a为实数,函数
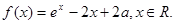
(I)求
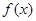 的单调区间与极值;
的单调区间与极值;(II)求证:当
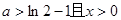 时,
时,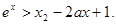
(I)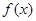 的单调递减区间是
的单调递减区间是 ,单调递增区间是
,单调递增区间是 ,
,
极小值为 (II)见解析。
(II)见解析。
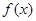 的单调递减区间是
的单调递减区间是 ,单调递增区间是
,单调递增区间是 ,
,极小值为
 (II)见解析。
(II)见解析。试题分析: (1)因为
 ,可知导数的大于零或者小于零的解集得到结论。
,可知导数的大于零或者小于零的解集得到结论。(2)构造函数设

于是
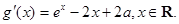 由(I)知当
由(I)知当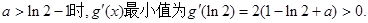 ,进而得到结论。
,进而得到结论。(I)解:由

令
 的变化情况如下表:
的变化情况如下表: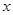 |  |  |  |
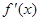 | — | 0 | + |
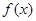 | 单调递减 |  |  单调递增 单调递增 |
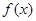 的单调递减区间是
的单调递减区间是 ,单调递增区间是
,单调递增区间是 ,
, 处取得极小值,
处取得极小值,极小值为

(II)证:设

于是
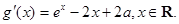
由(I)知当


于是当

而

即

点评:解决该试题的关键是熟练掌握求解函数单调性的三步骤,并求函数的极值,进而得到函数的最值问题的运用。

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
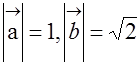 。
。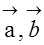 的夹角为
的夹角为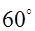 ,求
,求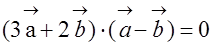 ,求
,求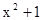 在(1,2)处的切线斜率为( )
在(1,2)处的切线斜率为( )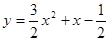 的某一切线与直线
的某一切线与直线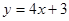 平行,则切点坐标
平行,则切点坐标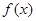 满足
满足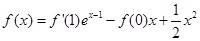 ,则
,则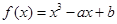 外的点A(1,0)作曲线C的切线恰有两条,
外的点A(1,0)作曲线C的切线恰有两条,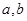 满足的等量关系;
满足的等量关系;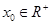 ,使
,使 成立,求
成立,求 的取值范围.
的取值范围.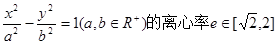 ,则一条渐近线与实轴所构成的角的取值范围是 .
,则一条渐近线与实轴所构成的角的取值范围是 . 的图象是折线段
的图象是折线段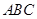 ,其中
,其中 的坐标分别为
的坐标分别为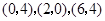 , 函数
, 函数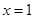 处的导数
处的导数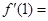 ________.
________. 
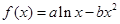 ,
,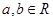
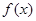 在
在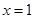 处与直线
处与直线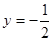 相切;
相切;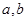 的值;②求函数
的值;②求函数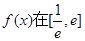 上的最大值;
上的最大值;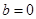 时,若不等式
时,若不等式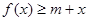 对所有的
对所有的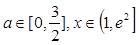 都成立,求实数
都成立,求实数 的取值范围.
的取值范围.