题目内容
(本小题满分14分)
已知函数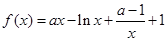 .
.
(1)当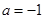 时,求曲线
时,求曲线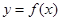 在点
在点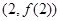 处的切线方程;
处的切线方程;
(2)当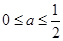 时,讨论
时,讨论 的单调性.
的单调性.
已知函数
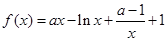 .
.(1)当
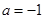 时,求曲线
时,求曲线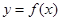 在点
在点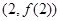 处的切线方程;
处的切线方程;(2)当
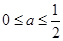 时,讨论
时,讨论 的单调性.
的单调性.(1) ;(2)当
;(2)当 时,函数
时,函数 在
在 上单调递增;函数
上单调递增;函数 在
在 上单调递减;当
上单调递减;当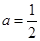 时,函数
时,函数 在
在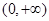 上单调递增;
上单调递增;
当 时,函数
时,函数 在
在 ,
, 上单调递增;函数
上单调递增;函数 在
在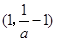 上单调递减
上单调递减
 ;(2)当
;(2)当 时,函数
时,函数 在
在 上单调递增;函数
上单调递增;函数 在
在 上单调递减;当
上单调递减;当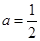 时,函数
时,函数 在
在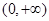 上单调递增;
上单调递增;当
 时,函数
时,函数 在
在 ,
, 上单调递增;函数
上单调递增;函数 在
在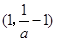 上单调递减
上单调递减本试题主要是考查了导数的几何意义的运用,以及函数单调性的判定的综合运用。
(1)因为当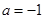 时,
时,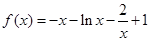 ,x∈(0,+∞),
,x∈(0,+∞),
∴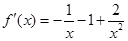 ,
, ,
,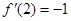 ,进而得到切线方程。
,进而得到切线方程。
(2)∵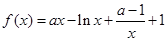 ,
,
∴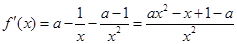 ,x∈(0,+∞),
,x∈(0,+∞),
令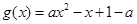 ,x∈(0,+∞).,对于参数a分情况讨论得到结论。
,x∈(0,+∞).,对于参数a分情况讨论得到结论。
解:(1)当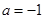 时,
时,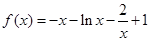 ,x∈(0,+∞), ……1分
,x∈(0,+∞), ……1分
∴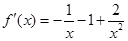 ,
, ,
,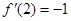 ,……4分
,……4分
所以切线方程为 ……5分
……5分
(2)∵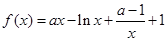 ,
,
∴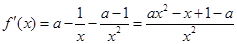 ,x∈(0,+∞),……7分
,x∈(0,+∞),……7分
令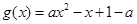 ,x∈(0,+∞).
,x∈(0,+∞).
① 当 时,
时, ,x∈(0,+∞),所以
,x∈(0,+∞),所以
当 时,
时,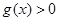 ,此时
,此时 ,函数
,函数 在
在 上单调递增;
上单调递增;
当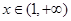 时,
时,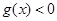 ,此时
,此时 ,函数
,函数 在
在 上单调递减;……9分
上单调递减;……9分
② 当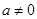 时,由
时,由 ,解得
,解得 ,
, .
.
ⅰ)若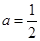 ,
, ,即
,即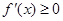 恒成立,函数
恒成立,函数 在
在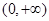 上单调递增; ……11分
上单调递增; ……11分
ⅱ)若 ,则
,则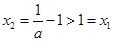 ,
,
当 时,
时,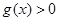 ,此时
,此时 ,函数
,函数 在
在 上单调递增;
上单调递增;
当 时,
时,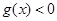 ,此时
,此时 ,函数
,函数 在
在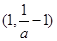 上单调递减;
上单调递减;
当 时,
时,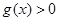 ,此时
,此时 ,函数
,函数 在
在 上单调递增;
上单调递增;
……14分
综上所述:当 时,函数
时,函数 在
在 上单调递增;函数
上单调递增;函数 在
在 上单调递减;
上单调递减;
当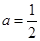 时,函数
时,函数 在
在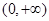 上单调递增;
上单调递增;
当 时,函数
时,函数 在
在 ,
, 上单调递增;函数
上单调递增;函数 在
在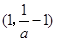 上单调递减
上单调递减
……14分
(1)因为当
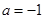 时,
时,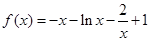 ,x∈(0,+∞),
,x∈(0,+∞),∴
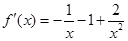 ,
, ,
,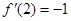 ,进而得到切线方程。
,进而得到切线方程。(2)∵
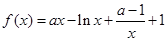 ,
,∴
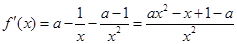 ,x∈(0,+∞),
,x∈(0,+∞),令
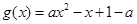 ,x∈(0,+∞).,对于参数a分情况讨论得到结论。
,x∈(0,+∞).,对于参数a分情况讨论得到结论。解:(1)当
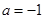 时,
时,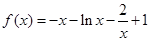 ,x∈(0,+∞), ……1分
,x∈(0,+∞), ……1分∴
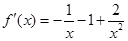 ,
, ,
,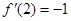 ,……4分
,……4分所以切线方程为
 ……5分
……5分(2)∵
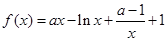 ,
,∴
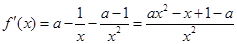 ,x∈(0,+∞),……7分
,x∈(0,+∞),……7分令
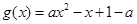 ,x∈(0,+∞).
,x∈(0,+∞).① 当
 时,
时, ,x∈(0,+∞),所以
,x∈(0,+∞),所以当
 时,
时,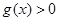 ,此时
,此时 ,函数
,函数 在
在 上单调递增;
上单调递增;当
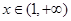 时,
时,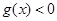 ,此时
,此时 ,函数
,函数 在
在 上单调递减;……9分
上单调递减;……9分② 当
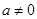 时,由
时,由 ,解得
,解得 ,
, .
.ⅰ)若
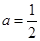 ,
, ,即
,即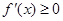 恒成立,函数
恒成立,函数 在
在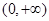 上单调递增; ……11分
上单调递增; ……11分ⅱ)若
 ,则
,则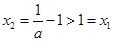 ,
,当
 时,
时,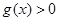 ,此时
,此时 ,函数
,函数 在
在 上单调递增;
上单调递增;当
 时,
时,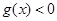 ,此时
,此时 ,函数
,函数 在
在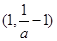 上单调递减;
上单调递减;当
 时,
时,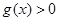 ,此时
,此时 ,函数
,函数 在
在 上单调递增;
上单调递增;……14分
综上所述:当
 时,函数
时,函数 在
在 上单调递增;函数
上单调递增;函数 在
在 上单调递减;
上单调递减;当
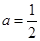 时,函数
时,函数 在
在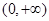 上单调递增;
上单调递增;当
 时,函数
时,函数 在
在 ,
, 上单调递增;函数
上单调递增;函数 在
在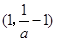 上单调递减
上单调递减……14分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
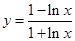 的导数是 ( )
的导数是 ( )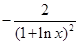
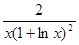
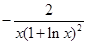
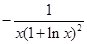
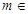 R,函数
R,函数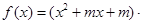 e
e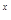 .
. 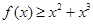 .
.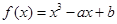 外的点A(1,0)作曲线C的切线恰有两条,
外的点A(1,0)作曲线C的切线恰有两条,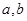 满足的等量关系;
满足的等量关系;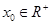 ,使
,使 成立,求
成立,求 的取值范围.
的取值范围.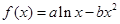 ,
,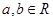
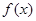 在
在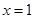 处与直线
处与直线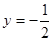 相切;
相切;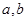 的值;②求函数
的值;②求函数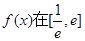 上的最大值;
上的最大值;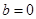 时,若不等式
时,若不等式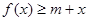 对所有的
对所有的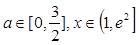 都成立,求实数
都成立,求实数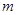 的取值范围.
的取值范围.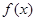 是最小正周期为
是最小正周期为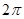 的偶函数,
的偶函数,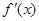 是
是 时,
时,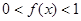 ;当
;当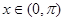 且
且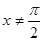 时 ,
时 ,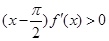 ,则函数
,则函数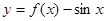 在
在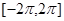 上的零点个数为( )
上的零点个数为( )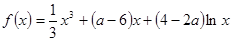 ,
,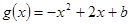
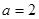 ,求
,求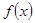 的单调区间;
的单调区间;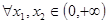 ,都有
,都有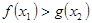 ,求实数
,求实数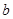 的取值范围;
的取值范围;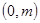 ,
,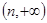 上单调递增,在
上单调递增,在 上单调递减,求实数
上单调递减,求实数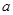 的取值范围。
的取值范围。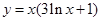 在点
在点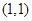 处的切线方程为__________________ .
处的切线方程为__________________ .