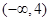题目内容
(本题12分)
已知函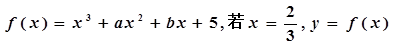 有极值,且曲线
有极值,且曲线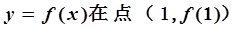 处的切线斜率为3.
处的切线斜率为3.
(1)求函数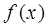 的解析式;
的解析式;
(2)求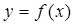 在[-4,1]上的最大值和最小值。
在[-4,1]上的最大值和最小值。
(3)函数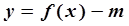 有三个零点,求实数
有三个零点,求实数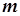 的取值范围.
的取值范围.
已知函
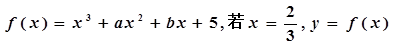 有极值,且曲线
有极值,且曲线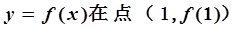 处的切线斜率为3.
处的切线斜率为3.(1)求函数
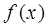 的解析式;
的解析式;(2)求
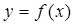 在[-4,1]上的最大值和最小值。
在[-4,1]上的最大值和最小值。(3)函数
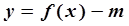 有三个零点,求实数
有三个零点,求实数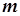 的取值范围.
的取值范围.(1)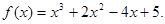
(2) 上的最大值为13,最小值为-11。
上的最大值为13,最小值为-11。
(3) 。
。
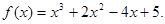
(2)
 上的最大值为13,最小值为-11。
上的最大值为13,最小值为-11。(3)
 。
。试题分析:(1)利用导数的几何意义得到参数a,b的值。
(2)求解导数判定函数的单调性,进而得到极值,和端点值,比较大小得到最值。
(3)根据函数单调性,确定极大值和极小值的符号,使得有三个零点。
解:(1)
 ……………………1分
……………………1分由题意,得
 …………3分
…………3分所以,
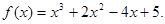 …………………………4分
…………………………4分(2)由(1)知

令
 ……………………5分
……………………5分| x | -4 | (-4, -2) | -2 | (-2, ) ) |  | ( ,1) ,1) | 1 |
 | | + | 0 | - | 0 | + | |
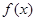 | | ↗ | 极大值 | ↘ | 极小值 | ↗ | |
| 函数值 | --11 | | 13 | |  | | 4 |
 上的最大值为13,最小值为-11。………9分
上的最大值为13,最小值为-11。………9分(3)
 ……………………………………12分
……………………………………12分点评:解决该试题的关键利用导数的符号判定函数的单调性进而确定其最值。

练习册系列答案
相关题目
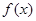 满足满足
满足满足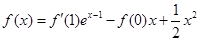 ;
;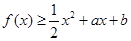 ,求
,求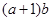 的最大值.
的最大值.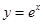 在点
在点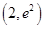 处的切线与坐标轴所围三角形的面积为 .
处的切线与坐标轴所围三角形的面积为 .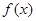 满足
满足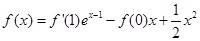 ,则
,则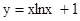
 在点
在点 处的切线平行于直线
处的切线平行于直线 ,则点
,则点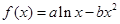 ,
,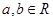
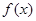 在
在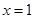 处与直线
处与直线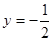 相切;
相切;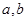 的值;②求函数
的值;②求函数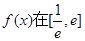 上的最大值;
上的最大值;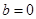 时,若不等式
时,若不等式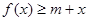 对所有的
对所有的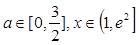 都成立,求实数
都成立,求实数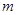 的取值范围.
的取值范围.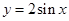 在点
在点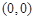 处的切线与直线
处的切线与直线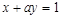 垂直,则实数
垂直,则实数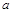 的值为( )
的值为( )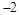
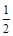
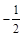
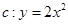 ,点
,点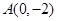 及点
及点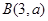 ,从点A观察B,要实现不被曲线C挡住,则实数
,从点A观察B,要实现不被曲线C挡住,则实数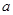 的取值范围是( )
的取值范围是( )