题目内容
函数f(x)=-(cos x)lg|x|的部分图像是( )
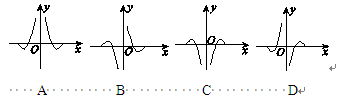

A
∵f(x)=-(cos x)lg|x|,
∴f(-x)=-[cos(-x)]lg|-x|=-(cos x)lg|x|=f(x)(x≠0),
∴函数f(x)=-(cos x)lg|x|为偶函数,故其图像关于y轴对称,可排除B,D;
又当0<x<1时,cos x>0,lg|x|<0,
∴当0<x<1时,f(x)=-(cos x)lg|x|>0,故可排除C.
故选A
∴f(-x)=-[cos(-x)]lg|-x|=-(cos x)lg|x|=f(x)(x≠0),
∴函数f(x)=-(cos x)lg|x|为偶函数,故其图像关于y轴对称,可排除B,D;
又当0<x<1时,cos x>0,lg|x|<0,
∴当0<x<1时,f(x)=-(cos x)lg|x|>0,故可排除C.
故选A

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 满足
满足 ,且当
,且当 时,
时,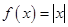 ,则
,则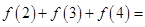 .
. 在
在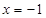 处有极值,则
处有极值,则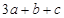 的值为 .
的值为 .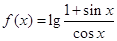 的图象( )
的图象( ) x对称
x对称 ,则f(-1)=________.
,则f(-1)=________. ,则f(-1)=( ).
,则f(-1)=( ).