题目内容
【题目】已知![]() ,
,![]() .
.
(1)若![]() ,命题“p∨q”为真,求实数
,命题“p∨q”为真,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 是
是![]() 的必要不充分条件,求实数
的必要不充分条件,求实数![]() 的取值范围.
的取值范围.
【答案】(1)[﹣4,2);(2) [﹣4,1]
【解析】
(1)根据复合命题真假关系进行转化求当命题“p∨q”为假时的范围即可.
(2)根据必要不充分条件与集合包含关系进行转化求解即可.
(1)若m=2时,p:﹣4≤x≤1,q:﹣1<x<2,
p∨q为真时,p、q两个命题一真一假或两个都为真,其对立事件为两个都为假,当p假且q假时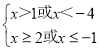 ,即x≥2或x<﹣4,
,即x≥2或x<﹣4,
所以p∨q为真时﹣4≤x<2,即x的取值范围为[﹣4,2);
(2)若p是q的必要不充分条件,则q的解集![]() p的解集,
p的解集,
①q=时,即m=﹣1时,满足题意;
②q≠时,当m>﹣1时p:﹣4≤x≤1,q:﹣1<x<m,因为q的解集![]() p的解集,所以m≤1.即-1<m≤1
p的解集,所以m≤1.即-1<m≤1
当m<﹣1时p:﹣4≤x≤1,q:m<x<﹣1,因为q的解集![]() p的解集,所以-1>m≥﹣4.
p的解集,所以-1>m≥﹣4.
综上﹣4≤m≤1;
综上,实数m的取值范围为[﹣4,1].

练习册系列答案
相关题目