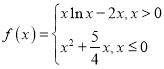题目内容
【题目】已知函数f (x)=ax﹣ex(a∈R),g(x)=![]() .
.
(Ⅰ)求函数f (x)的单调区间;
(Ⅱ)x0∈(0,+∞),使不等式f (x)≤g(x)﹣ex成立,求a的取值范围.
【答案】(Ⅰ)答案见解析(Ⅱ)![]()
【解析】
试题(Ⅰ)f′(x)=a﹣ex,x∈R.对a分类讨论,利用导数研究函数的单调性即可得出;
(Ⅱ)由x0∈(0,+∞),使不等式f(x)≤g(x)﹣ex,即a≤![]() .设h(x)=
.设h(x)=![]() ,则问题转化为a
,则问题转化为a![]() ,利用导数研究函数的单调性极值与最值即可得出.
,利用导数研究函数的单调性极值与最值即可得出.
解:(Ⅰ)∵f′(x)=a﹣ex,x∈R.
当a≤0时,f′(x)<0,f(x)在R上单调递减;
当a>0时,令f′(x)=0得x=lna.
由f′(x)>0得f(x)的单调递增区间为(﹣∞,lna);
由f′(x)<0得f(x)的单调递减区间为(lna,+∞).
(Ⅱ)∵x0∈(0,+∞),使不等式f(x)≤g(x)﹣ex,则![]() ,即a≤
,即a≤![]() .
.
设h(x)=![]() ,则问题转化为a
,则问题转化为a![]() ,
,
由h′(x)=![]() ,令h′(x)=0,则x=
,令h′(x)=0,则x=![]() .
.
当x在区间(0,+∞) 内变化时,h′(x)、h(x)变化情况如下表:

由上表可知,当x=![]() 时,函数h(x)有极大值,即最大值为
时,函数h(x)有极大值,即最大值为![]() .
.
∴![]() .
.

【题目】已知椭圆![]() 、抛物线
、抛物线![]() 的焦点均在
的焦点均在![]() 轴上,
轴上,![]() 的中心和
的中心和![]() 的顶点均为原点
的顶点均为原点![]() ,从每条曲线上取两个点,将其坐标记录于下表中:
,从每条曲线上取两个点,将其坐标记录于下表中:
| 3 |
| 4 |
|
|
| 0 |
|
|
(Ⅰ)求![]() 的标准方程;
的标准方程;
(Ⅱ)请问是否存在直线![]() 满足条件:①过
满足条件:①过![]() 的焦点
的焦点![]() ;②与
;②与![]() 交不同两点
交不同两点![]() 且满足
且满足![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
【题目】近年电子商务蓬勃发展,现从某电子商务平台评价系统中随机选出200次成功交易,并对其评价进行统计,统计结果显示:网购者对商品的满意率为0.70,对快递的满意率为0.60,其中对商品和快递都满意的交易为80次.
(1)根据已知条件完成下面的2×2列联表,并回答在犯错误的概率不超过0.10的前提下,能否认为“网购者对商品满意与对快递满意之间有关系”?
对快递满意 | 对快递不满意 | 合计 | |
对商品满意 | 80 | ||
对商品不满意 | |||
合计 | 200 |
(2)为进一步提高购物者的满意度,平台按分层抽样方法从200次交易中抽取10次交易进行问卷调查,详细了解满意与否的具体原因,并在这10次交易中再随机抽取2次进行电话回访,听取购物者意见.求电话回访的2次交易至少有一次对商品和快递都满意的概率.
附: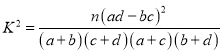 (其中
(其中![]() 为样本容量)
为样本容量)
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【题目】跨年迎新联欢晚会简称跨年晚会,是指每年阳历年末12月31日晚上各电视台和政府为喜迎新而精心策划的演唱会活动,跨年晚会首次出现在港台地区,跨年晚会因形式和举办地不同因而名称也不同,如央视启航2020跨年盛典,湖南卫视跨年演唱会,东方卫视迎新晚会等.某电视台为了了解2020年举办的跨年迎新晚会观众的满意度,现分别随机选出![]() 名观众对迎新晚会的质量评估评分,最高分为
名观众对迎新晚会的质量评估评分,最高分为![]() 分,综合得分情况如下表所示:
分,综合得分情况如下表所示:
综合得分 |
|
|
|
|
|
|
|
观众人数 | 5 | 10 | 25 | 30 | 15 | 10 | 5 |
根据表中的数据,回答下列问题:
(1)根据表中的数据,绘制这![]() 位观众打分的频率分布直方图;
位观众打分的频率分布直方图;
(2)已知观众的评分![]() 近似服从
近似服从![]() ,其中
,其中![]() 是反应随机变量
是反应随机变量![]() 取值的平均水平的特征数,工作人员在分析数据时发现,可用
取值的平均水平的特征数,工作人员在分析数据时发现,可用![]() 位观众评分的平均数估计
位观众评分的平均数估计![]() ,但由于评分观众人数较少,误差较大,所以不能直接用
,但由于评分观众人数较少,误差较大,所以不能直接用![]() 位观众评分的标准差的值估计
位观众评分的标准差的值估计![]() ,而在这
,而在这![]() 位观众打分的频率分布直方图的基础上依据
位观众打分的频率分布直方图的基础上依据![]() 来估计
来估计![]() 更科学合理,试求
更科学合理,试求![]() 和
和![]() 的估计值(
的估计值(![]() 的结果精确到小数点后两位).
的结果精确到小数点后两位).