题目内容
【题目】已知函数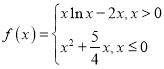 的图象上有且仅有两个不同的点关于直线
的图象上有且仅有两个不同的点关于直线![]() 的对称点在
的对称点在![]() 的图象上,则实数
的图象上,则实数![]() 的取值范围是________.
的取值范围是________.
【答案】![]()
【解析】
求出直线![]() 关于直线
关于直线![]() 对称的直线
对称的直线![]() 的方程
的方程![]() ,然后将问题转化为直线
,然后将问题转化为直线![]() 与函数
与函数![]() 的图象有两个交点,构造函数
的图象有两个交点,构造函数 ,将问题转化为直线
,将问题转化为直线![]() 与函数
与函数![]() 的图象有两个交点,利用数形结合思想可求出实数
的图象有两个交点,利用数形结合思想可求出实数![]() 的取值范围.
的取值范围.
直线![]() 关于直线
关于直线![]() 对称的直线
对称的直线![]() 的方程为
的方程为![]() ,即
,即![]() ,对应的函数为
,对应的函数为![]() .
.
所以,直线![]() 与函数
与函数![]() 的图象有两个交点.
的图象有两个交点.
对于一次函数![]() ,当
,当![]() 时,
时,![]() ,且
,且![]() .
.
则直线![]() 与函数
与函数![]() 的图象交点的横坐标不可能为
的图象交点的横坐标不可能为![]() .
.
当![]() 时,令
时,令![]() ,可得
,可得![]() ,
,
此时,令 .
.
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
此时,函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
函数![]() 的极小值为
的极小值为![]() ;
;
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
此时,函数![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减,
上单调递减,
函数![]() 的极大值为
的极大值为![]() .
.
作出函数![]() 和函数
和函数![]() 的图象如下图所示:
的图象如下图所示:
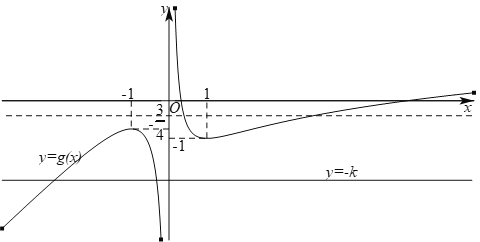
由图象可知,当![]() 或
或![]() 时,即当
时,即当![]() 或
或![]() 时,直线
时,直线![]() 与函数
与函数![]() 的图象有两个交点.
的图象有两个交点.
因此,实数![]() 的取值范围是
的取值范围是![]() .
.
故答案为:![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目