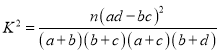题目内容
【题目】设![]() 是定义在
是定义在![]() 上的周期函数,周期
上的周期函数,周期![]() ,对
,对![]() 都有
都有![]() ,且当
,且当![]() 时,
时,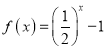 ,若在区间
,若在区间![]() 内关于
内关于![]() 的方程
的方程![]() 恰有3个不同的实根,则
恰有3个不同的实根,则![]() 的取值范围是
的取值范围是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
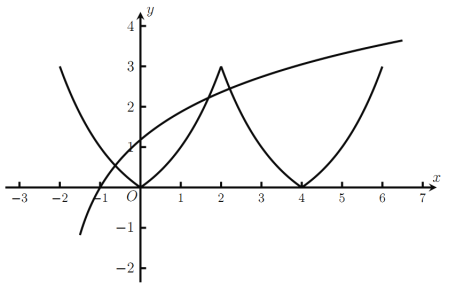
结合函数的奇偶性、函数的周期性和函数的解析式绘制函数f(x)的图像,原问题等价于函数y=f(x)与y=loga(x+2)在区间(2,6]上有三个不同的交点,数形结合有loga4<3,且loga8>3,求解不等式即可确定实数a的取值范围.
∵对x∈R都有f(x)=f(x),∴函数f(x)是定义在R上的偶函数,
在区间(2,6]内关于x的方程f(x)loga(x+2)=0恰有3个不同的实数解,
∴函数y=f(x)与y=loga(x+2)在区间(2,6]上有三个不同的交点,
∵当x∈[2,0]时,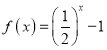 ,
,
故函数图像如图所示,
又f(2)=f(2)=f(6)=3,
则有loga4<3,且loga8>3,
解得:![]() .
.
故a的取值范围是![]() .
.
故选:D.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目