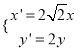题目内容
【题目】已知
是双曲线
的右焦点，
是
左支上一点，
），当
周长最小时，则点的纵坐标为（ ）
A. 
B. 
C. 
D. 
【答案】B
【解析】
左焦点E（-3，0）,△APF周长最小|PA|+|PF|最小|PA|+|PE|+2最小P在线段AE上．
如图：
由双曲线C的方程可知：a2=1，b2=8，∴c2=a2+b2=1+8=9，∴c=3，∴左焦点E（-3，0），右焦点F（3，0），
∵|AF|=
，所以当三角形APF的周长最小时，|PA|+|PF|最小．
由双曲线的性质得|PF|-|PE|=2a=2，∴|PF|=|PE|+2，
又|PE|+|PA|≥|AE|=|AF|=15，当且仅当A，P，E三点共线时，等号成立．
∴三角形APF的周长：|AF|+|AP|+|PF|=15+|PE|+|AP|+2≥15+15+2=32．
此时，直线AE的方程为y=
，将其代入到双曲线方程得：x2+9x+14=0，
解得x=-7（舍）或x=-2，
由x=-2得y=2
（负值已舍）
故选：B．
练习册系列答案
相关题目
【题目】已知某地区中小学生人数和近视情况如图1和图2所示.为了解该地区中小学生的近视形成原因，用分层抽样的方法抽取2%的学生作为样本进行调查.
（1）求样本容量和抽取的高中生近视人数分别是多少？
（2）在抽取的
名高中生中，平均每天学习时间超过9小时的人数为
，其中有12名学生近视，请完成高中生平均每天学习时间与近视的列联表：
平均学习时间不超过9小时 | 平均学习时间超过9小时 | 总计 | |
不近视 | |||
近视 | |||
总计 |
（3）根据（2）中的列联表，判断是否有
的把握认为高中生平均每天学习时间与近视有关？
附：
，其中
.
