题目内容
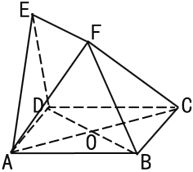
【题目】如图所示,等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 中点,
中点,![]() 与
与![]() 交于点
交于点![]() ,将
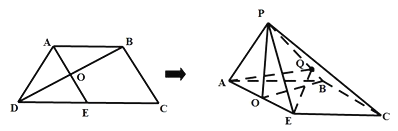
,将![]() 沿
沿![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置(
的位置(![]() 平面
平面![]() ).
).
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,试判断线段
,试判断线段![]() 上是否存在一点
上是否存在一点![]() (不含端点),使得直线
(不含端点),使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(1)证明见解析(2)存在,![]()
【解析】
(1)先利用线面垂直的判定定理证明![]() 平面
平面![]() ,再利用面面垂直证明面
,再利用面面垂直证明面![]() 平面
平面![]() 即可;
即可;
(2)建立空间直角坐标系求出平面![]() 的法向量,再利用向量所成角的关系式求出直线
的法向量,再利用向量所成角的关系式求出直线![]() 与平面
与平面![]() 所成角的正弦值,建立关系式,即可得出
所成角的正弦值,建立关系式,即可得出![]() 的值.
的值.
(1)证明:连接![]() ,在等腰梯形中
,在等腰梯形中![]() ,
,![]() ,
,![]() ,
,![]() 为中点,
为中点,
∴四边形![]() 为菱形,∴
为菱形,∴![]() ,
,
∴![]() ,
,![]() ,即
,即![]() ,
,![]() ,且
,且![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
(2)由(1)可知四边形![]() 为菱形,∴
为菱形,∴![]() ,
,
在等腰梯形![]() 中
中![]() ,∴
,∴![]() 正三角形,
正三角形,
∴![]() ,同理
,同理![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() .
.
由(1)可知![]() ,
,![]() ,
,
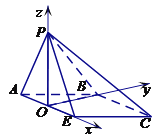
以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 分别为
分别为![]() 轴,
轴,![]() 轴,为
轴,为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,
,
由题意得,各点坐标为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
设![]() ,
,![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则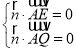 ,即
,即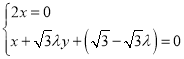 ,
,
取![]() ,
,![]() ,得
,得![]() ,∴
,∴![]() ,
,
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,![]() ,
,
则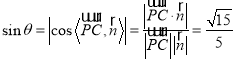 ,即
,即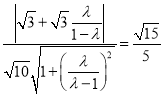 ,
,
化简得:![]() ,解得
,解得![]() ,
,
∴存在点![]() 为
为![]() 的中点时,使直线
的中点时,使直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
【题目】已知某校运动会男生组田径综合赛以选手三项运动的综合积分高低决定排名.具体积分规则如表1所示,某代表队四名男生的模拟成绩如表2.
表1 田径综合赛项目及积分规则
项目 | 积分规则 |
| 以 |
跳高 | 以 |
掷实心球 | 以 |
表2 某队模拟成绩明细
姓名 | 100米跑(秒) | 跳高(米) | 掷实心球(米) |
甲 |
|
|
|
乙 |
|
|
|
丙 |
|
|
|
丁 |
|
|
|
根据模拟成绩,该代表队应选派参赛的队员是:( )
A.甲B.乙C.丙D.丁