题目内容
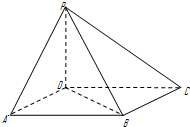如图，四棱锥P-ABCD中，底面ABCD为平行四边形，∠DAB=60°，AB=2AD=2，PD⊥底面ABCD，且PD=AD，求：平面PAB的一个法向量．
练习册系列答案
相关题目
若直线ax+by+c=0与抛物线y2=2x交于P，Q两点，F为抛物线的焦点，直线PF，QF分别交抛物线于点M，N，则直线MN的方程为（ ）
| A、4cx-2by+a=0 | B、ax-2by+4c=0 | C、4cx+2by+a=0 | D、ax+2by+4c=0 |
下面使用的类比推理中恰当的是（ ）
| A、“若m•2=n•2，则m=n”类比得出“若m•0=n•0，则m=n” | ||||||
| B、“（a+b）c=ac+bc”类比得出“（a•b）c=ac•bc” | ||||||
C、“（a+b）c=ac+bc”类比得出“
| ||||||
| D、“（pq）n=pn•qn”类比得出“（p+q）n=pn+qn” |
复数z=
（i为虚数单位），则|z|等于（ ）
| 3-i |
| i |
| A、10 | ||
B、
| ||
| C、5 | ||
D、
|
如图，AO⊥平面α，O为垂足，B∈α，BC⊥BO，BC与平面α所成的角为30°，AO=BO=BC=1，则AC的长等于将甲、乙在内的7名工人分成3个小组，一组3人，另两组每组各2人，则甲乙不分在同一组的分法有（ ）
| A、80 | B、170 | C、185 | D、65 |
二项式（2+x2）（1-x）6的展开式中x2的系数为（ ）
| A、28 | B、31 | C、35 | D、38 |
如图，四边形ABCD内接于圆O，∠BOD=110°，∠BCD等于（ ）
| A、100° | B、110° | C、125° | D、135° |