题目内容
二项式(2+x2)(1-x)6的展开式中x2的系数为( )
| A、28 | B、31 | C、35 | D、38 |
考点:二项式系数的性质
专题:二项式定理
分析:把(1-x)6 按照二项式定理展开,可得二项式(2+x2)(1-x)6的展开式中x2的系数.
解答:解:由于二项式(2+x2)(1-x)6=(2+x2)(1-6x+15x2-20x3+15x4-6x5+x6),
∴展开式中x2的系数为 2×15+1=31,
故选:B.
∴展开式中x2的系数为 2×15+1=31,
故选:B.
点评:本题主要考查二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于基础题.

练习册系列答案
相关题目
给出下列函数:
①f(x)=x
;
②f(x)=2x;
③f(x)=log2x;
④f(x)=sinx.
则满足关系式f′(
)>f(
)-f(
)>f′(
)的函数的序号是( )
①f(x)=x
| 1 |
| 2 |
②f(x)=2x;
③f(x)=log2x;
④f(x)=sinx.
则满足关系式f′(
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| A、①③ | B、②④ |
| C、①③④ | D、②③④ |
i为虚数单位,(
)2=( )
| 1-i |
| 1+i |
| A、1 | B、-1 | C、i | D、-i |
在二项式(
+
)n的展开式中只有第五项的二项式系数最大,把展开式中所有的项重新排成一列,则有理项都互不相邻的概率为( )
| x |
| 2 | |||
|
A、
| ||
B、
| ||
C、
| ||
D、
|
若函数f(x)=|x+2|+|x-3|的最小值为n,则二项式(x2+
)n的展开式中的常数项是( )
| 2 | ||
|
| A、第3项 | B、第4项 |
| C、第5项 | D、第6项 |
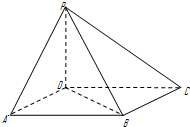 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD=2,PD⊥底面ABCD,且PD=AD,求:平面PAB的一个法向量.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD=2,PD⊥底面ABCD,且PD=AD,求:平面PAB的一个法向量.