题目内容
在直角坐标系xOy中,直线C1的参数方程为C1:
(t为参数);以O为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2.
(1)求曲线C2的直角坐标方程,说明它表示什么曲线,并写出其参数方程;
(2)过直线C1上的点向曲线ρ=1作切线,求切线长的最小值.
|
(1)求曲线C2的直角坐标方程,说明它表示什么曲线,并写出其参数方程;
(2)过直线C1上的点向曲线ρ=1作切线,求切线长的最小值.
练习册系列答案
相关题目
在极坐标系中,曲线C:p=2cosθ上任意一点P到点Q(
,
)的最大距离等于( )
| 2 |
| π |
| 4 |
A、
| ||
| B、2 | ||
C、
| ||
D、
|
参数方程
(t为参数)表示的曲线不在( )
|
| A、x轴的上方 |
| B、x轴的下方 |
| C、y轴的左侧 |
| D、y轴的右侧 |
-1+2i是下列哪个实系数方程的一个根( )
| A、x2-4x+5=0 | B、x2+4x+5=0 | C、x2-2x+5=0 | D、x2+2x+5=0 |

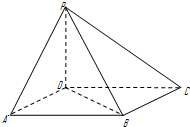 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD=2,PD⊥底面ABCD,且PD=AD,求:平面PAB的一个法向量.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD=2,PD⊥底面ABCD,且PD=AD,求:平面PAB的一个法向量. 则实数a的取值范围是_____________.
则实数a的取值范围是_____________.