题目内容
若直线ax+by+c=0与抛物线y2=2x交于P，Q两点，F为抛物线的焦点，直线PF，QF分别交抛物线于点M，N，则直线MN的方程为（ ）
| A、4cx-2by+a=0 | B、ax-2by+4c=0 | C、4cx+2by+a=0 | D、ax+2by+4c=0 |
练习册系列答案
导学教程高中新课标系列答案
小学课时特训系列答案
相关题目
已知命题p：?x∈R，cosx=
；命题q：?x∈R，x2-x+1＞0．则下列结论正确的是（ ）
| 5 |
| 4 |
| A、命题p∨q是假命题 |
| B、命题p∧q是真命题 |
| C、命题（￢p）∧（￢q）是真命题 |
| D、命题（￢p）∨（￢q）是真命题 |
已知直线l1：ax+3y-1=0，l2：x+by+1=0，则
=-3是l1⊥l2（ ）
| a |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
经过抛物线C的焦点F作直线l与抛物线C交于A，B两点，如果A，B在抛物线C的准线上的射影分别为A1、B1，那么∠A1FB1为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
若抛物线y2=2px（p＞0）与直线x-y-1=0相交于A，B两点，且
•
=-1，则p=（ ）
| OA |
| OB |
| A、1 | B、2 | C、4 | D、8 |
给出下列函数：
①f（x）=x
；
②f（x）=2x；
③f（x）=log2x；
④f（x）=sinx．
则满足关系式f′（
）＞f（
）-f（
）＞f′（
）的函数的序号是（ ）
①f（x）=x
| 1 |
| 2 |
②f（x）=2x；
③f（x）=log2x；
④f（x）=sinx．
则满足关系式f′（
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| A、①③ | B、②④ |
| C、①③④ | D、②③④ |
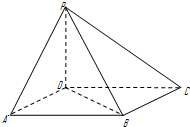如图，四棱锥P-ABCD中，底面ABCD为平行四边形，∠DAB=60°，AB=2AD=2，PD⊥底面ABCD，且PD=AD，求：平面PAB的一个法向量．