Question

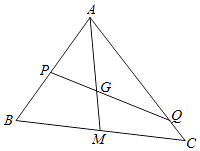
【题目】设G为△ABC的重心，过G作直线l分别交线段AB，AC（不与端点重合）于P，Q．若 =λ ， =μ
（1）求 + 的值；
（2）求λμ的取值范围．

Answer 1

【答案】
（1）解：连结AG并延长交BC于M，则M是BC的中点，则 ， ．

又 ， ，

∴ = ， =（ ） + ．

∵P，G，Q三点共线，故存在实数t，使 =t ，即（ ） + = ．

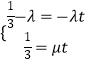∴ ，两式相除消去t得1﹣3λ=﹣ ，即 ．

（2）解：∵1﹣3λ=﹣ ，∴ ，

∵λ，μ∈（0，1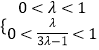），∴ ，解得 ．∴ ．

∴λμ= = ．

∴当 时，λμ取得最小值 ，当 或2时，λμ取得最大值 ．

∴λμ的取值范围是[ ， ）．

【解析】（1）使用 表示出 ，根据P，Q，G三点共线得出λ，μ的关系；（2）用λ表示出μ，令λ，μ∈（0，1）得出λ的范围，则λμ可表示为关于λ的函数，求出该函数的最值即可．
【考点精析】解答此题的关键在于理解平面向量的基本定理及其意义的相关知识，掌握如果、是同一平面内的两个不共线向量，那么对于这一平面内的任意向量，有且只有一对实数、，使．