题目内容
【题目】已知集合A={x|1＜x≤5}，集合B={ 
＞0}．
（1）求A∩B；
（2）若集合C={x|a+1≤x≤4a﹣3}，且C∪A=A，求实数a的取值范围．
【答案】
（1）解：由 
得（2x﹣1）（x﹣3）＞0，
解得x＜ 
或x＞3，则集合B={x|x＜ 或x＞3}，
因集合A={x|1＜x≤5}，
所以A∩B={x|3＜x≤5}
（2）解：因为C∪A=A，所以CA={x|1＜x≤5}，
又集合C={x|a+1≤x≤4a﹣3}，
①当C=时，则4a﹣3＜a+1，解得 
，满足题意；
②当C≠时，要使CA，则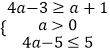 
，解得 
．
综上所述，实数a的取值范围为（﹣∞，2]
【解析】（1）由分式不等式的解法求出集合B，由交集的运算求出A∩B；（2）由C∪A=A得CA，根据子集的定义对C进行分类讨论，分别列出不等式组，求出实数a的取值范围．
【考点精析】解答此题的关键在于理解集合的交集运算的相关知识，掌握交集的性质：（1）A∩B
A，A∩BB，A∩A=A，A∩
=,A∩B=B∩A;（2）若A∩B=A，则AB，反之也成立．
【题目】某厂商为了解用户对其产品是否满意，在使用产品的用户中随机调查了80人，结果如下表：
（1）根据上述，现用分层抽样的方法抽取对产品满意的用户5人，在这5人中任选2人，求被选中的恰好是男、女用户各1人的概率；
（2）有多大把握认为用户对该产品是否满意与用户性别有关？请说明理由.
| 0.15 | 0．10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
注：
【题目】某单位共有10名员工，他们某年的收入如下表：
员工编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
年薪（万元） | 4 | 4.5 | 6 | 5 | 6.5 | 7.5 | 8 | 8.5 | 9 | 51 |
（1）求该单位员工当年年薪的平均值和中位数；
（2）从该单位中任取2人，此2人中年薪收入高于7万的人数记为
，求
的分布列和期望；
（3）已知员工年薪收入与工作年限成正相关关系，某员工工作第一年至第四年的年薪分别为4万元，5.5万元，6万元，8.5万元，预测该员工第五年的年薪为多少？
附：线性回归方程
中系数计算公式分别为：
， 
，其中
为样本均值.
