题目内容
【题目】在直角坐标系中，以坐标原点O为极点，x轴的非负半轴为极轴建立极坐标系，直线l的极坐标方程为ρsin（θ+
）=
，曲线C的参数方程为
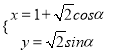（α为参数）．
（1）求直线l的普通方程；
（2）若P是曲线C上的动点，求点P到直线l的最大距离及点P的坐标．
【答案】（1）x+y﹣5=0．（2）P（0，﹣1）．距离最大值
．
【解析】试题分析：（1）根据
将直线l的极坐标方程化为直角坐标方程（2）根据点到直线距离公式得三角函数关系式，再根据三角函数有界性确定最大值以及对应点P的坐标．
试题解析：解：（1）直线l的极坐标方程为ρsin（θ+
）=
，
展开可得：
（sinθ+cosθ）=，
可得x+y﹣5=0．
（2）曲线C的参数方程为
（α为参数）．可设P（1+
cosα，sinα）．
则点P到直线l的距离d=
=2﹣sin
，
当sin=﹣1时，d取得最大值3
．
取α=
，可得P（0，﹣1）．
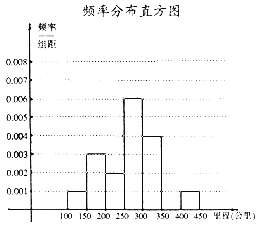
小学生10分钟口算测试100分系列答案
【题目】面对全球范围内日益严峻的能源形势与环保压力，环保与低碳成为今后汽车发展的一大趋势，越来越多的消费者对新能源汽车表示出更多的关注，某研究机构从汽车市场上随机抽取N辆纯电动汽车调查其续航里程（单次充电后能行驶的最大里程），被调查汽车的续航里程全部介于100公里和450公里之间，根据调查数据形成了如图所示频率分布表及频率分布直方图．
频率分布表
分组 | 频数 | 频率 |
[100，150） | 1 | 0.05 |
[150，200） | 3 | 0.15 |
[200，250） | x | 0.1 |
[250，300） | 6 | 0.3 |
[300，350） | 4 | 0.2 |
[350，400） | 3 | y |
[400，450] | 1 | 0.05 |
合计 | N | 1 |
（1）试确定频率分布表中x，y，N的值，并补全频率分布直方图；
（2）若从续航里程在[200，250）及[350，400）的车辆中随机抽取2辆车，求两辆车续航里程都在[350，400）的概率．
