题目内容
【题目】在平面直角坐标系xOy中,椭圆C的参数方程为![]() (θ为参数),直线l的参数方程为
(θ为参数),直线l的参数方程为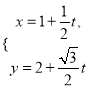 (t为参数).
(t为参数).
(Ⅰ)写出椭圆C的普通方程和直线l的倾斜角;
(Ⅱ)若点P(1,2),设直线l与椭圆C相交于A,B两点,求|PA|·|PB|的值.
【答案】(I) ![]() ;(Ⅱ)
;(Ⅱ) ![]() .
.
【解析】试题分析:(Ⅰ)利用平方法消去θ得到椭圆C的普通方程为![]() ,根据直线参数方程的几何意义求出直线的斜率,从而可得结果;(Ⅱ)把直线
,根据直线参数方程的几何意义求出直线的斜率,从而可得结果;(Ⅱ)把直线![]() 的方程
的方程 ,代入
,代入![]() 中,利用直线参数方程的几何意义求出直线的斜率结合韦达定理可得结果.
中,利用直线参数方程的几何意义求出直线的斜率结合韦达定理可得结果.
试题解析:(Ⅰ)消去θ得到椭圆C的普通方程为![]() .
.
∵直线![]() 的斜率为
的斜率为![]() ,∴直线l的倾斜角为
,∴直线l的倾斜角为![]() .
.
(Ⅱ)把直线![]() 的方程
的方程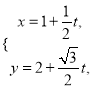 ,代入
,代入![]() 中,
中,
得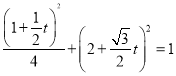 .
.
即![]() ,
,
∴t1·t2=4,即|PA|·|PB|=4.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
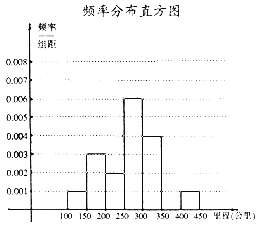
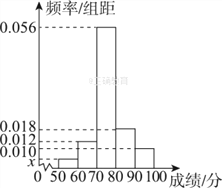
【题目】面对全球范围内日益严峻的能源形势与环保压力,环保与低碳成为今后汽车发展的一大趋势,越来越多的消费者对新能源汽车表示出更多的关注,某研究机构从汽车市场上随机抽取N辆纯电动汽车调查其续航里程(单次充电后能行驶的最大里程),被调查汽车的续航里程全部介于100公里和450公里之间,根据调查数据形成了如图所示频率分布表及频率分布直方图.
频率分布表
分组 | 频数 | 频率 |
[100,150) | 1 | 0.05 |
[150,200) | 3 | 0.15 |
[200,250) | x | 0.1 |
[250,300) | 6 | 0.3 |
[300,350) | 4 | 0.2 |
[350,400) | 3 | y |
[400,450] | 1 | 0.05 |
合计 | N | 1 |
(1)试确定频率分布表中x,y,N的值,并补全频率分布直方图;
(2)若从续航里程在[200,250)及[350,400)的车辆中随机抽取2辆车,求两辆车续航里程都在[350,400)的概率.