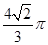题目内容
如图,在四边形ABCD中,AC平分∠DAB,∠ABC=60°,AC=6,AD=5,S△ADC=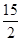 ,求AB的长.
,求AB的长.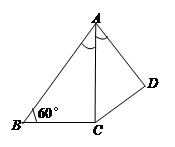
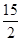 ,求AB的长.
,求AB的长.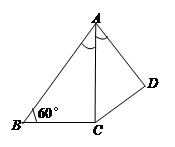

试题分析:在△ADC中,已知AC=6,AD=5,S△ADC=
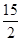 ,
,则由S△ADC=
 ·AC·AD·sin∠DAC,求得sin∠DAC=
·AC·AD·sin∠DAC,求得sin∠DAC= ,即∠DAC=30°,
,即∠DAC=30°,∴ ∠BAC=30°.
而∠ABC=60°,故△ABC为直角三角形.
∵ AC=6,∴ AB=
 .
.点评:解决此类问题的关键是找到合适的三角形,在三角形中利用正弦定理、余弦定理、勾股定理和三角形的面积公式等求解.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 中,
中, ,
, ,
, 为
为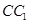 的中点,则异面直线
的中点,则异面直线 与
与 所成角的余弦值为
所成角的余弦值为



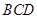 是等边三角形,
是等边三角形, 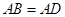 ,
,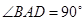 ,
,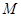 ,
,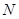 ,
,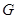 分别是
分别是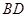 ,
,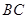 ,
,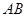 的中点,将△
的中点,将△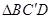 的位置,使得
的位置,使得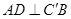 .
.
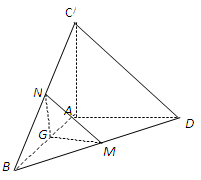
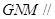 平面
平面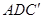 ;
;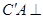 平面
平面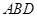 .
.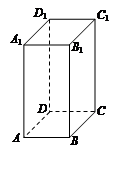
 中
中 ,
, 面
面 ,
, ,
, 面
面 .
.
 是两个不同的平面,给出下列四个命题
是两个不同的平面,给出下列四个命题 ②
②
 ④若
④若
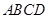 中,
中,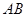 ,
,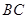 ,
,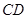 两两互相垂直,且
两两互相垂直,且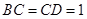 .
.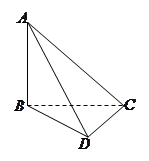
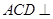 平面
平面 ;
;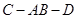 的大小;
的大小;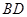 与平面
与平面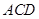 所成的角为
所成的角为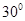 ,求线段
,求线段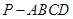 中,侧棱都相等,底面是边长为
中,侧棱都相等,底面是边长为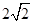 的正方形,底面中心为
的正方形,底面中心为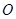 ,以
,以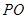 为直径的球经过侧棱中点,则该球的体积为( )
为直径的球经过侧棱中点,则该球的体积为( )