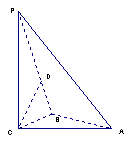
题目内容
在长方体ABCD-A1B1C1D1中,AB=1,AD=2.若存在各棱长均相等的四面体P1P2P3P4,其中P1,P2,P3,P4分别在棱AB,A1B1,C1D1,CD所在的直线上,则此长方体的体积为 .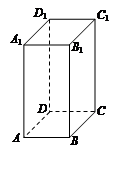
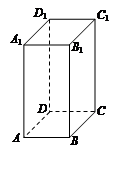
4
试题分析:由题意可知,棱AB,A1B1,C1D1,CD所在的直线应为某个正四棱锥所在的直线,因为AD=2,所以A1A=2,所以此长方体的体积为
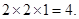
点评:解答此题时,根据正四面体是由正方体截掉四个角得到的,分析出A1A=AD,是解答的关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
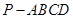 的底面
的底面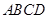 是边长为2的菱形,
是边长为2的菱形,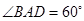 .已知
.已知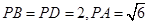 .
.
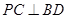
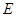 为
为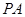 的中点,求三菱锥
的中点,求三菱锥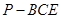 的体积.
的体积. 是三条不同的直线,
是三条不同的直线, 是三个不同的平面,则下列命题不正确的是( )
是三个不同的平面,则下列命题不正确的是( ) ∥
∥ ,
, ,则
,则 ∥
∥ ,
, ,则
,则
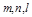 是三条不同的直线,
是三条不同的直线, 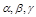 是三个不同的平面,
是三个不同的平面, 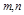 与
与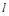 都垂直,则
都垂直,则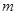 ∥
∥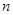
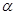 ,
,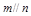 ,则
,则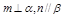 且
且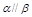 ,则
,则
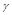 与平面
与平面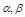 所成的角相等,则
所成的角相等,则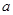 表示一条直线,则M内至少有一直线与
表示一条直线,则M内至少有一直线与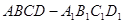 的面对角线
的面对角线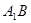 上存在一点
上存在一点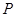 使得
使得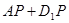 最短,则
最短,则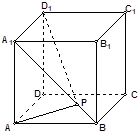



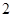
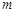 、
、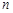 是不同的直线,
是不同的直线,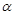 、
、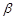 、
、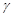 是不同的平面,以下四个命题为真命题的是
是不同的平面,以下四个命题为真命题的是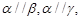 则
则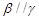 ②若
②若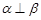 ,
,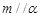 ,则
,则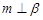
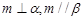 ,则
,则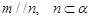 ,则
,则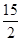 ,求AB的长.
,求AB的长.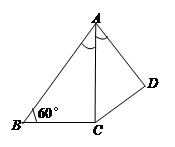
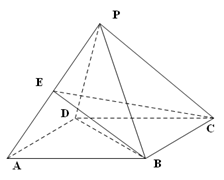
 平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD
平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD