题目内容
已知 中
中 ,
, 面
面 ,
, ,
,
求证: 面
面 .
.
 中
中 ,
, 面
面 ,
, ,
,求证:
 面
面 .
.
根据线线垂直来证明线面垂直,是一般的证明线面垂直的方法之一,该试题只要证明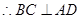
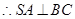 即可。
即可。
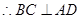
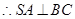 即可。
即可。试题分析:证明:
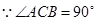
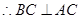
又
 面
面
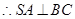
 面
面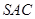
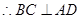
又
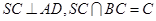
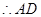
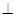 面
面
点评:主要是考查了三棱锥性质的运用,以及线面垂直的判定证明,属于基础题。

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
题目内容
 中
中 ,
, 面
面 ,
, ,
, 面
面 .
.
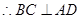
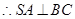 即可。
即可。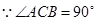
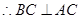
 面
面
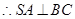
 面
面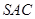
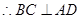
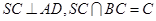
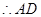
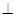 面
面

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案