题目内容
长方体 中,
中, ,
, ,
, 为
为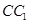 的中点,则异面直线
的中点,则异面直线 与
与 所成角的余弦值为
所成角的余弦值为
 中,
中, ,
, ,
, 为
为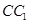 的中点,则异面直线
的中点,则异面直线 与
与 所成角的余弦值为
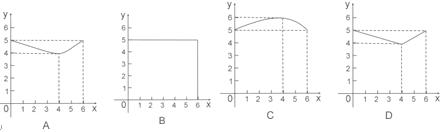
所成角的余弦值为A. | B. | C. | D. |
B
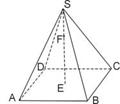
试题分析:建立空间直角坐标系,先相关点的坐标,再相关向量的坐标,再进行运算.解析:建立坐标系如图

则A(1,0,0),E(0,2,1),B(1,2,0),C1(0,2,2).=(-1,0,2),A=(-1,2,1),cos<BC1,AE>═

所以异面直线BC1与AE所成角的余弦值为
 ,故选B
,故选B点评:本题主要考查用向量法求异面直线所成的角,属于基础题。

练习册系列答案
相关题目
 ,求AB的长.
,求AB的长.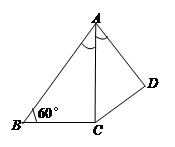
 平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD
平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD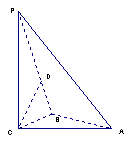
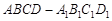 中,M、N分别是棱CD1、CC1的中点,则异面直线MA1与DN所成角的余弦值是 .
中,M、N分别是棱CD1、CC1的中点,则异面直线MA1与DN所成角的余弦值是 .
 的底面
的底面 为菱 形 ,AC∩BD=O侧棱
为菱 形 ,AC∩BD=O侧棱 ⊥BD,点F为
⊥BD,点F为 的中点.
的中点.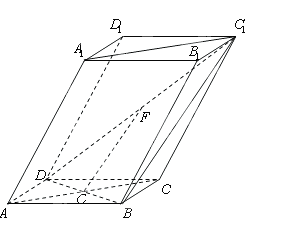
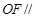 平面
平面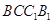 ;
;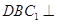 平面
平面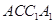 .
.  是以
是以 为直径的半圆上异于
为直径的半圆上异于 、
、 的点,矩形
的点,矩形 所在的平面垂直于该半圆所在的平面,且
所在的平面垂直于该半圆所在的平面,且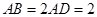 .
.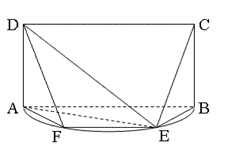
 ;
; 与半圆弧的另一个交点为
与半圆弧的另一个交点为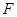 .
. ;
; ,求三棱锥
,求三棱锥 的体积.
的体积. 中,侧棱与底面垂直,
中,侧棱与底面垂直, ,
, ,点
,点 分别为
分别为 和
和 的中点.
的中点.
 ;
; 的正弦值.
的正弦值.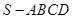 的底面边长为
的底面边长为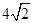 ,高
,高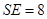 ,点
,点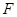 在高
在高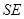 上,且
上,且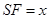 ,记过点
,记过点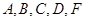 的球的半径为
的球的半径为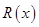 ,则函数
,则函数