题目内容
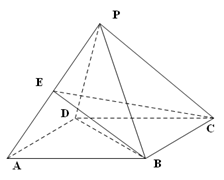
如图所示,在四面体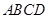 中,
中,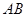 ,
,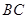 ,
,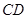 两两互相垂直,且
两两互相垂直,且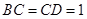 .
.
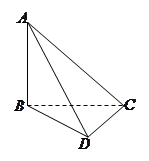
(1)求证:平面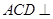 平面
平面 ;
;
(2)求二面角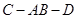 的大小;
的大小;
(3)若直线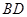 与平面
与平面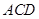 所成的角为
所成的角为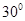 ,求线段
,求线段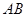 的长度.
的长度.
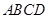 中,
中,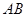 ,
,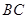 ,
,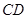 两两互相垂直,且
两两互相垂直,且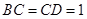 .
.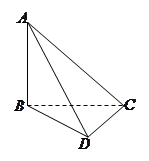
(1)求证:平面
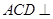 平面
平面 ;
;(2)求二面角
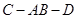 的大小;
的大小;(3)若直线
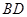 与平面
与平面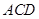 所成的角为
所成的角为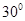 ,求线段
,求线段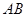 的长度.
的长度.(1)∵  ,
, ,∴
,∴  平面
平面 ,又
,又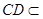 平面
平面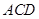 ,∴ 平面
,∴ 平面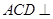 平面
平面 (2)
(2) (3)
(3)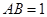
 ,
, ,∴
,∴  平面
平面 ,又
,又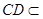 平面
平面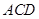 ,∴ 平面
,∴ 平面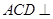 平面
平面 (2)
(2) (3)
(3)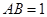
试题分析:(1)∵
 ,
, ,
,∴
 平面
平面 .
.又
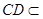 平面
平面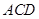 ,
,∴ 平面
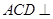 平面
平面 . 4分
. 4分(2)∵
 ,
,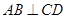 ,∴
,∴ 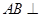 平面
平面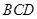 .
.∴
 .
.∴
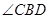 是二面角
是二面角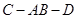 的平面角. 6分
的平面角. 6分在
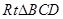 中,∵
中,∵ 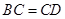 ,∴
,∴  .
.∴ 二面角
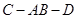 的大小为
的大小为 . 8分
. 8分(3)过点
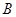 作
作
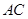 ,垂足为
,垂足为 ,连接
,连接 .
.∵ 平面
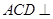 平面
平面 , ∴
, ∴  平面
平面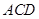 ,
,∴
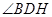 为
为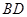 与平面
与平面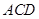 所成的角.
所成的角.∴
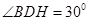 . 10分
. 10分在
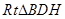 中,
中,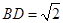 ,∴
,∴  .
.又∵在
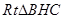 中,
中,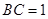 ,∴
,∴  ,
,∴ 在
 中,
中,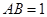 . 12分
. 12分点评:面面垂直的判定主要利用垂直的判定定理和性质定理,本题中的二面角线面角求解时现根据定义做出相应的角,再通过解三角形求出角的大小

练习册系列答案
相关题目
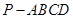 的底面
的底面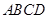 是边长为2的菱形,
是边长为2的菱形,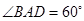 .已知
.已知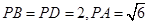 .
.
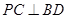
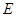 为
为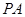 的中点,求三菱锥
的中点,求三菱锥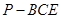 的体积.
的体积.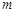 、
、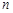 是不同的直线,
是不同的直线,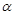 、
、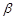 、
、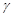 是不同的平面,以下四个命题为真命题的是
是不同的平面,以下四个命题为真命题的是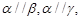 则
则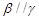 ②若
②若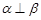 ,
,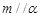 ,则
,则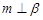
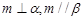 ,则
,则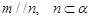 ,则
,则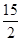 ,求AB的长.
,求AB的长.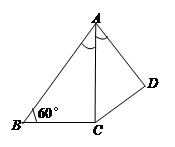
 中,
中, ,且
,且 ,
, 平面
平面 ,过
,过 作截面分别交
作截面分别交 于
于 ,且二面角
,且二面角 的大小为
的大小为 ,则截面
,则截面 面积的最小值为 .
面积的最小值为 .
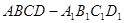 中
中 ,
, 分别是
分别是 的中点,
的中点, 在棱
在棱 上,且
上,且 .
.
 ; (2)求二面角
; (2)求二面角 的大小.
的大小. EA=EC=6,M为EC中点,平面BCE⊥平面ACE,AE⊥EB
EA=EC=6,M为EC中点,平面BCE⊥平面ACE,AE⊥EB
 平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD
平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD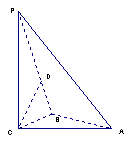
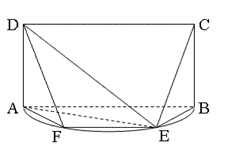
 是以
是以 为直径的半圆上异于
为直径的半圆上异于 、
、 的点,矩形
的点,矩形 所在的平面垂直于该半圆所在的平面,且
所在的平面垂直于该半圆所在的平面,且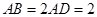 .
.
 ;
; 与半圆弧的另一个交点为
与半圆弧的另一个交点为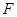 .
. ;
; ,求三棱锥
,求三棱锥 的体积.
的体积.