题目内容
已知四棱锥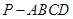 中,侧棱都相等,底面是边长为
中,侧棱都相等,底面是边长为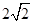 的正方形,底面中心为
的正方形,底面中心为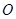 ,以
,以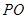 为直径的球经过侧棱中点,则该球的体积为( )
为直径的球经过侧棱中点,则该球的体积为( )
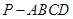 中,侧棱都相等,底面是边长为
中,侧棱都相等,底面是边长为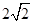 的正方形,底面中心为
的正方形,底面中心为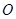 ,以
,以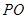 为直径的球经过侧棱中点,则该球的体积为( )
为直径的球经过侧棱中点,则该球的体积为( )A. | B.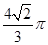 | C. | D. |
C
试题分析:如图,G为侧棱PB的中点,结合题意得
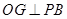 ,所以
,所以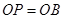 ,又因为
,又因为 ,所以
,所以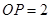 ,球的半径为1,其体积为
,球的半径为1,其体积为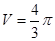 。故选C。
。故选C。
点评:求几何体的表面积和体积是常考知识点,我们要知道柱体、锥体和球的表面积公式和体积公式。

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
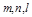 是三条不同的直线,
是三条不同的直线, 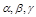 是三个不同的平面,
是三个不同的平面, 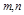 与
与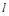 都垂直,则
都垂直,则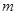 ∥
∥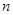
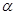 ,
,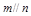 ,则
,则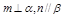 且
且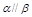 ,则
,则
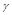 与平面
与平面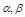 所成的角相等,则
所成的角相等,则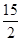 ,求AB的长.
,求AB的长.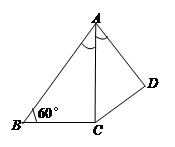
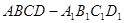 中
中 ,
, 分别是
分别是 的中点,
的中点, 在棱
在棱 上,且
上,且 .
.
 ; (2)求二面角
; (2)求二面角 的大小.
的大小. EA=EC=6,M为EC中点,平面BCE⊥平面ACE,AE⊥EB
EA=EC=6,M为EC中点,平面BCE⊥平面ACE,AE⊥EB
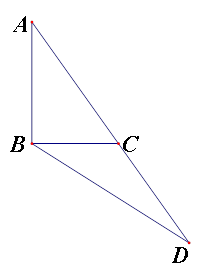
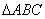 中,
中,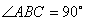 ,延长
,延长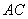 到
到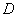 ,连接
,连接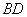 ,若
,若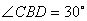 ,且
,且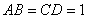 ,则
,则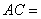 ________.
________.
 平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD
平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD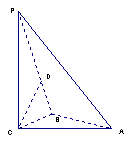
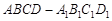 中,M、N分别是棱CD1、CC1的中点,则异面直线MA1与DN所成角的余弦值是 .
中,M、N分别是棱CD1、CC1的中点,则异面直线MA1与DN所成角的余弦值是 . 中,侧棱与底面垂直,
中,侧棱与底面垂直, ,
, ,点
,点 分别为
分别为 和
和 的中点.
的中点.
 ;
; 的正弦值.
的正弦值.