题目内容
已知函数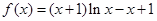 .
.
(Ⅰ)若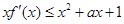 ,求
,求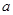 的取值范围;
的取值范围;
(Ⅱ)证明: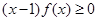 .
.
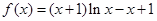 .
.(Ⅰ)若
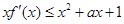 ,求
,求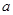 的取值范围;
的取值范围;(Ⅱ)证明:
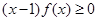 .
.(Ⅰ)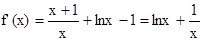 , ………………2分
, ………………2分
xf′(x)=xlnx+1,
题设xf′(x)≤x2+ax+1等价于lnx-x≤a,
令g(x)=lnx-x,则g’(x)=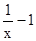 。 ………………4分
。 ………………4分
当0<x<1时,g’(x)>0;当x≥1时,g’(x)≤0,x=1是g(x)的最大值点,
g(x)≤g(1)=-1。 ………………6分
综上,a的取值范围是[-1,+∞)。 ………………7分
(Ⅱ)由(Ⅰ)知,g(x)≤g(1)=-1,即lnx-x+1≤0;
当0<x<1时,f(x)=(x+1)lnx-x+1=xlnx+(lnx-x+1)≤0;………10分
当x≥1时,f(x)=lnx+(xlnx-x+1)
=lnx+x(lnx+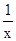 -1)≥0
-1)≥0
所以(x-1)f(x)≥0
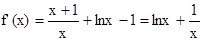 , ………………2分
, ………………2分xf′(x)=xlnx+1,
题设xf′(x)≤x2+ax+1等价于lnx-x≤a,
令g(x)=lnx-x,则g’(x)=
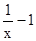 。 ………………4分
。 ………………4分当0<x<1时,g’(x)>0;当x≥1时,g’(x)≤0,x=1是g(x)的最大值点,
g(x)≤g(1)=-1。 ………………6分
综上,a的取值范围是[-1,+∞)。 ………………7分
(Ⅱ)由(Ⅰ)知,g(x)≤g(1)=-1,即lnx-x+1≤0;
当0<x<1时,f(x)=(x+1)lnx-x+1=xlnx+(lnx-x+1)≤0;………10分
当x≥1时,f(x)=lnx+(xlnx-x+1)
=lnx+x(lnx+
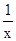 -1)≥0
-1)≥0所以(x-1)f(x)≥0
略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
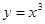 过点(2, 8)的切线方程;
过点(2, 8)的切线方程;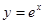 过点(0,0)的切线方程。
过点(0,0)的切线方程。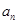 是函数
是函数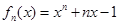 的零点,
的零点,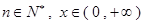 .
.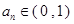 ,且
,且
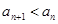 ;
;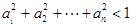 .
.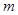 米,余下工程只需要建两端桥墩之间的桥面和桥墩,经预测,建一个桥墩的工程费用为256万元,距离为
米,余下工程只需要建两端桥墩之间的桥面和桥墩,经预测,建一个桥墩的工程费用为256万元,距离为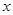 米的相邻两桥墩之间的桥面工程费用为
米的相邻两桥墩之间的桥面工程费用为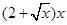 万元。假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为
万元。假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为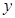 万元。
万元。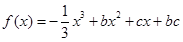 ,其导函数
,其导函数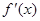 .
. 试确定b、c的值;
试确定b、c的值;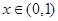 时,函数
时,函数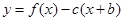 的图象上任一点P处的切线斜率为k,若
的图象上任一点P处的切线斜率为k,若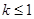 ,求实数b的取值范围。
,求实数b的取值范围。 在(0,2)内单调递减,则实数a的取值范围
在(0,2)内单调递减,则实数a的取值范围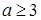
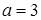
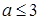
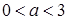
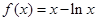 的单调递减区间为( )
的单调递减区间为( )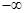 ,1)
,1) )
) 则
则
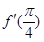 的值为____________.
的值为____________.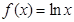 在
在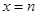
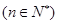 处的切线斜率为
处的切线斜率为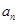 ,
,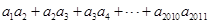 = .
= .